定義
廣義容斥原理是容斥原理的變形或推廣。
 廣義容斥原理
廣義容斥原理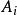 廣義容斥原理
廣義容斥原理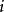 廣義容斥原理
廣義容斥原理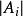 廣義容斥原理
廣義容斥原理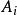 廣義容斥原理
廣義容斥原理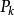 廣義容斥原理
廣義容斥原理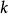 廣義容斥原理
廣義容斥原理設有與性質1,2,...,n相關的元素 個, 為滿足第 種性質的所有元素的集合,假定 表示集合 的元素個數,定義 為至少有 種性質的元素的元次,則有:
 廣義容斥原理
廣義容斥原理 廣義容斥原理
廣義容斥原理,
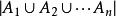 廣義容斥原理
廣義容斥原理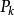 廣義容斥原理
廣義容斥原理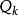 廣義容斥原理
廣義容斥原理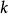 廣義容斥原理
廣義容斥原理容斥原理利用 解決了如何求解 和 的問題。
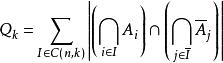 廣義容斥原理
廣義容斥原理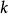 廣義容斥原理
廣義容斥原理下定義 為恰好有種性質的元素的元次,即:
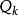 廣義容斥原理
廣義容斥原理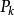 廣義容斥原理
廣義容斥原理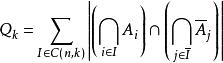 廣義容斥原理
廣義容斥原理廣義容斥原理則告訴了 與 兩者之間的關係如下:
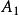 廣義容斥原理
廣義容斥原理例如:
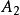 廣義容斥原理
廣義容斥原理 廣義容斥原理
廣義容斥原理舉例
某校有12個教師,已知教數學的有8位,教物理的有6位,教化學的5位;數、理5位,數、化4位,理、化3位;數理化3位。問教其他課的有幾位?只教一門的有幾位?正好教兩門的有幾位?
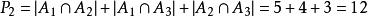 廣義容斥原理
廣義容斥原理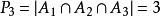 廣義容斥原理
廣義容斥原理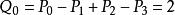 廣義容斥原理
廣義容斥原理解:令教數學的教師屬於 ,教物理的屬於 ,教化學的屬於 。
則
 廣義容斥原理
廣義容斥原理 廣義容斥原理
廣義容斥原理,
所以根據題目要求:
(1)教其他課的:
(2)只教一門的:
 廣義容斥原理
廣義容斥原理(3)正好教兩門的:

