帕斯卡三角形[三角形矩陣]

楊輝三角，是二項式係數在三角形中的一種幾何排列，中國南宋數學家楊輝1261年所著的《詳解九章算法》一書中出現。在歐洲，帕斯卡（1623----1662）在1654年發現這一規律，所以這個表又叫做帕斯卡三角形。帕斯卡的發現比楊輝要遲393年，比賈憲遲600年。

楊輝三角是中國數學史上的一個偉大成就。

簡介

楊輝三角，是二項式係數在三角形中的一種幾何排列。在歐洲，這個表叫做帕斯卡三角形。帕斯卡（1623----1662）是在1654年發現這一規律的，比楊輝要遲393年，比賈憲遲600年。楊輝三角是中國古代數學的傑出研究成果之一，它把二項式係數圖形化，把組合數內在的一些代數性質直觀地從圖形中體現出來，是一種離散型的數與形的結合。

帕斯卡三角形[三角形矩陣]

概述

前提：每行端點與結尾的數為1.

（與上圖中的n不同，這裡第一行定義為n=1）

1.每個數等於它上方兩數之和。

2.每行數字左右對稱，由1開始逐漸變大。

3.第n行的數字有n項。

4.第n行的m個數可表示為 C(n-1，m-1)，即為從n-1個不同元素中取m-1個元素的組合數。

5.第n行的第m個數和第n-m+1個數相等 ，為組合數性質之一。

6.每個數字等於上一行的左右兩個數字之和。可用此性質寫出整個楊輝三角。即第n+1行的第i個數等於第n行的第i-1個數和第i個數之和，這也是組合數的性質之一。即 C(n+1,i)=C(n,i)+C(n,i-1)。

7.(a+b)的展開式中的各項係數依次對應楊輝三角的第(n+1)行中的每一項。

8.將第2n+1行第1個數，跟第2n+2行第3個數、第2n+3行第5個數……連成一線，這些數的和是第4n+1個斐波那契數；將第2n行第2個數(n>1)，跟第2n-1行第4個數、第2n-2行第6個數……這些數之和是第4n-2個斐波那契數。

9.將第n行的各數值，分別乘以10的列數m-1次方，然後把這些數值相加的和等於11的n-1次方。例子：第11行數分別為1,10,45,120,210,252,210,120,45,10,1，則11^10 = 1*10^0+10*10^1+45*10^2+...+1*10^10 =25937424601

套用

性質5和性質7是楊輝三角的基本性質，是研究楊輝三角其他規律的基礎。

帕斯卡三角形[三角形矩陣]

與楊輝三角聯繫最緊密的是二項式乘方展開式的係數規律，即二項式定理。例如在楊輝三角中，第3行的三個數恰好對應著兩數和的平方的展開式的每一項的係數（性質 8），第4行的四個數恰好依次對應兩數和的立方的展開式的每一項的係數，即 ，以此類推。

帕斯卡三角形[三角形矩陣]

又因為性質5：第n行的m個數可表示為C(n-1,m-1)，即為從n-1個不同元素中取m-1個元素的組合數。因此可得出二項式定理的公式為：

因此，二項式定理與楊輝三角形是一對天然的數形趣遇，它把數形結合帶進了計算數學。求二項式展開式係數的問題，實際上是一種組合數的計算問題。用係數通項公式來計算，稱為“式算”；用楊輝三角形來計算，稱作“圖算”。

數在楊輝三角中的出現次數

由1開始，正整數在楊輝三角形出現的次數為∞,1, 2, 2, 2, 3, 2, 2, 2, 4, 2, 2, 2, 2, 4, ... （OEIS:A003016）。最小而又大於1的數在賈憲三角形至少出現n次的數為2, 3, 6, 10, 120, 120, 3003, 3003, ... （OEIS:A062527）

除了1之外，所有正整數都出現有限次，只有2出現剛好一次，6,20,70等出現三次；出現兩次和四次的數很多，還未能找到出現剛好五次的數。120,210,1540等出現剛好六次。（OEIS:A098565）

帕斯卡三角形[三角形矩陣]

帕斯卡三角形[三角形矩陣]

因為丟番圖方程 有無窮個解，所以出現至少六次的數有無窮個多。解為 ，其中F表示第n個斐波那契數（F=F=1）。

3003是第一個出現八次的數。

歷史沿革

北宋人賈憲約1050年首先使用“賈憲三角”進行高次開方運算。

楊輝，字謙光，南宋時期杭州人。在他1261年所著的《詳解九章算法》一書中，輯錄了如上所示的三角形數表，稱之為“開方作法本源”圖，並說明此表引自11世紀中葉（約公元1050年）賈憲的《釋鎖算術》，並繪畫了“古法七乘方圖”。故此，楊輝三角又被稱為“賈憲三角”。

元朝數學家朱世傑在《四元玉鑒》（1303年）擴充了“賈憲三角”成“古法七乘方圖”。

義大利人稱之為“塔塔利亞三角形”（Triangolo di Tartaglia）以紀念在16世紀發現一元三次方程解的塔塔利亞。

在歐洲直到1623年以後，法國數學家帕斯卡在13歲時發現了“帕斯卡三角”。

布萊士·帕斯卡的著作Traité du triangle arithmétique（1655年）介紹了這個三角形。帕斯卡蒐集了幾個關於它的結果，並以此解決一些機率論上的問題，影響面廣泛，Pierre Raymond de Montmort（1708年）和亞伯拉罕·棣·美弗（1730年）都用帕斯卡來稱呼這個三角形。

21世紀以來國外也逐漸承認這項成果屬於中國，所以有些書上稱這是“中國三角形”（Chinese triangle）

歷史上曾經獨立繪製過這種圖表的數學家有：

•賈憲 中國北宋 11世紀 《釋鎖算術》

•楊輝 中國南宋1261《詳解九章算法》記載之功

•朱世傑 中國元代 1299《四元玉鑒》級數求和公式

•阿爾·卡西 阿拉伯 1427《算術的鑰匙》

•阿皮亞納斯 德國 1527

•米歇爾.斯蒂費爾 德國 1544《綜合算術》二項式展開式係數

•薛貝爾 法國 1545

•B·帕斯卡 法國 1654《論算術三角形》

其實，中國古代數學家在數學的許多重要領域中處於遙遙領先的地位。中國古代數學史曾經有自己光輝燦爛的篇章，而楊輝三角的發現就是十分精彩的一頁。

在編程中實現

楊輝三角在編程實現中較為容易。最常見的算法便是用上一行遞推計算；也有運用和組合的對應關係而使用階乘計算的，然而後者速度較慢且階乘容易溢出。編程的輸出大多相類，此處並不過多添加截圖。

C、C++、C#、Java 語言之間的語法也大多相類，因此這裡也不會將每一種算法都在這些語言中各實現一遍。要在這些語言的版本間修改，實際上只需注意一些簡單的語法和函式名稱的改變，如 C 的 int yh[M][M] 應改寫為 Java 的 int[][] yh = new int[M][M]、C# 的 int[,] yh=new int[M,M]；C printf 應使用 Java 的 System.out.print、C# 的 Console.Write 、C++ 中更智慧型的 cout 來替換。

C++

Bash

Bash 輸出楊輝三角並使用 nl 表明行號

C#

C

以下的代碼均用標準 C 語言寫成，可以被包括 MSVC（含 VC6）、GCC 的多種 C 編譯器編譯。

這個算法使用只行列位置和左側的數值算出數值：

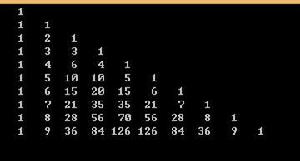默認狀態下不啟用金字塔和菱形的輸出

默認求直角三角形，可通過注釋的開關或使用編譯器的 -D 定義開關調節等腰三角形和菱形輸出。如果覺得複雜，可按照 define 使用的情況剔除因不符合 ifdef 條件從而未啟用的代碼之後閱讀。

這個算法創建了一個二維數組，並且通過上一行的數值求當前行。在反過來再次列印時，這個程式會使用以前算好的值，從而節省了重複疊代的時間。

這一個使用大數組寫成，風格更接近教科書上的 VC6 代碼。

這個版本使用佇列的方式輸出。

Visual Basic

單擊視窗在彈出輸入框後輸入行數後按確認 就能在窗體上列印楊輝三角了

SQL

易語言

來自易語言自帶的例子。

以下為全文。

Java

PHP

只輸出數組的方式如下：

Python

較為便捷，代碼量較少的實現方式如下：

該方式用到了列表生成式，理解起來較困難，下面是另一種方式：

另一個不用生成器的版本：