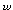對偶理論
正文
發展簡史 線上性規劃早期發展中最重要的發現就是對偶問題，即每一個線性規劃問題(稱為原始問題)都有一個與它對應的對偶線性規劃問題（稱為對偶問題）。1928年美籍匈牙利數學家 J.von諾伊曼在研究對策論時已發現線性規劃與對策論之間存在著密切的聯繫。兩人零和對策可表達成線性規劃的原始問題和對偶問題。他於1947年提出對偶理論。1951年G.B.丹齊克引用對偶理論求解線性規劃的運輸問題，研究出確定檢驗數的位勢法原理。1954年C.萊姆基提出對偶單純形法，成為管理決策中進行靈敏度分析的重要工具。對偶理論有許多重要套用：在原始的和對偶的兩個線性規劃中求解任何一個規劃時，會自動地給出另一個規劃的最優解；當對偶問題比原始問題有較少約束時，求解對偶規劃比求解原始規劃要方便得多；對偶規劃中的變數就是影子價格。對偶問題 每一個線性規劃問題都伴隨有另一個線性規劃問題，稱為對偶問題。原來的線性規劃問題則稱為原始線性規劃問題，簡稱原始問題。對偶問題有許多重要的特徵，它的變數能提供關於原始問題最優解的許多重要資料，有助於原始問題的求解和分析。對偶問題與原始問題之間存在著下列關係：①目標函式對原始問題是極大化，對對偶問題則是極小化。②原始問題目標函式中的收益係數是對偶問題約束不等式中的右端常數，而原始問題約束不等式中的右端常數則是對偶問題中目標函式的收益係數。③原始問題和對偶問題的約束不等式的符號方向相反。④原始問題約束不等式係數矩陣轉置後即為對偶問題的約束不等式的係數矩陣。⑤原始問題的約束方程數對應於對偶問題的變數數，而原始問題的變數數對應於對偶問題的約束方程數。⑥對偶問題的對偶問題是原始問題，這一性質被稱為原始和對偶問題的對稱性。
基本定理 原始問題和對偶問題的標準形式如下：
原始問題對偶問題
maxz＝cxmin
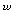＝ybs.t.Ax≤bs.t.yA≥c
x≥0y≥0
式中max表示求極大值,min表示求極小值,s.t.表示“約束條件為”；z為原始問題的目標函式，w為對偶問題的目標函式；x為原始問題的決策變數列向量（n×1），y為對偶問題的決策變數行向量(1×m);A為原始問題的係數矩陣(m×n),b為原始問題的右端常數列向量（m×1），c為原始問題的目標函式係數行向量（1×n）。在原始問題與對偶問題之間存在著一系列深刻的關係，業已得到嚴格數學證明的有如下一些定理。
弱對偶定理 若上述原始問題和對偶問題分別有可行解x0和y0,則y0b≥cx0。這個定理表明極大化問題任一可行解的目標函式值總是不大於它的對偶問題的任一可行解的目標函式值。
強對偶定理 若上述原始問題和對偶問題都可行，則它們分別有最優解x*和y*，且cx*=y*b。
最優準則定理 若上述原始問題和對偶問題分別有可行解x0和y0,且兩者的目標函式值相等，即y0b=cx0,則兩個可行解分別為對應線性規劃的最優解。
互補鬆弛定理 若上述原始問題和對偶問題分別有可行解x0和y0，且u0和v0分別為它們的鬆弛變數,則若且唯若v0x0+u0y0時，x0和y0分別為它們的最優解。
鬆弛定理 若上述原始問題和對偶問題分別有可行解x0和y0,且u0和v0分別為它們的鬆弛變數，則若且唯若v0x0=0 和u0y0=0時, x0和y0分別為它們的最優解。v0x0=0和u0y0=0這兩個等式稱為互補鬆弛條件。
對稱對偶線性規劃 具有對稱形式的線性規劃的特點是：①全部約束條件均為不等式，對極大化問題為≤，對極小化問題為≥。②全部變數均為非負。列出對稱對偶線性規劃的步驟是：①規定非負的對偶變數，變數數等於原始問題的約束方程數。②把原始問題的目標函式係數作為對偶問題約束不等式的右端常數。③把原始問題約束不等式的右端常數作為對偶問題的目標函式係數。④把原始問題的係數矩陣轉置後作為對偶問題的係數矩陣。⑤把原始問題約束條件中的不等號反向作為對偶問題約束條件的不等號。⑥將原始問題目標函式取極大化改成對偶問題目標函式取極小化。
非對稱對偶線性規劃
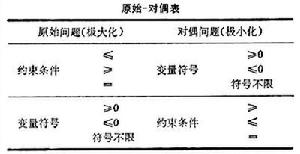有時線性規劃並不以對稱方式出現，如約束條件並不都是同向不等式，變數可以是非正的或沒有符號約束。列寫非對稱對偶線性規劃可參照原始-對偶表（見表）按下列步驟進行：①規定對偶變數，變數個數等於原始問題約束不等式數。②把原始問題的目標函式係數作為對偶問題約束不等式的右端常數。③把原始問題約束不等式的右端常數作為對偶問題的目標函式係數。④把原始問題的係數矩陣轉置後作為對偶問題的係數矩陣。⑤根據原始問題的約束不等式情況，確定對偶變數的符號約束。⑥根據原始問題決策變數的符號約束，確定對偶問題約束不等式的符號方向。 對偶問題的最優解 從原始問題的最終單純形表中（最優單純形運算元）可直接得到對偶問題的最優解。原始問題中鬆弛變數的檢驗數對應著對偶問題的解（符號相反）。在用單純形法時每一步疊代可得到原始問題的可行解x0和對偶問題的補充解y0,且cx0=y0b,若x0不是原始問題的最優解，y0就不是對偶問題的可行解。最後一步疊代得到原始問題的最優解x*和對偶問題的補充最優解y*，且cx*=y*b。y*是原始問題的影子價格。
