問題歸約法

問題規約法是一種基於狀態空間的問題描述與求解方法。 它是已知問題的描述，通過一系列變換把此問題變為一個子問題集合，這些子問題的解可以直接得到（本原問題），從而解決了初始問題的一種算法。

組成

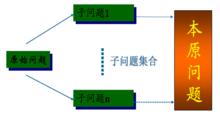問題歸約法

一個初始問題描述；

一套把問題變換為子問題的操作符；

一套本原問題描述。(本原問題:不能再分解或變換且直接可解的子問題)

實質

從目標（要解決的問題）出發逆向推理，建立子問題以及子問題的子問題，直到最後把初始問題歸約為一個本原問題集合。這些本原問題的解可以直接得到從而解決了初始問題，用與或圖來有效地說明問題歸約法的求解途徑。問題歸約法能夠比狀態空間法更有效地表示問題。狀態空間法是問題歸約法的一種特例。在問題歸約法的與或圖中，包含有與節點和或節點，而在狀態空間法中只含有或節點 。

基本思路

套用一系列算符將原始問題的描述變換或分解成為子問題的描述問題的描述可以採用各種數據結構，如表、樹、矢量、數組等。

典型實例

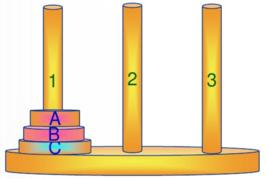
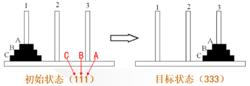問題歸約法

漢諾塔問題（ Hanoi ）

（1）從1移到3 ；

（2）每次移動一個盤子；

（3）大盤在下小盤在上 。