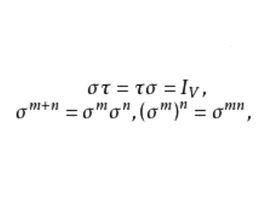可逆線性變換的定義
設σ是線性空間V的一個線性變換，如果存在V的另一個變換τ，使得
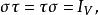可逆線性變換則稱線性變換σ為可逆的，並稱τ為σ的逆。
顯然，當σ可逆時，它的逆是唯一的，將σ的唯一逆記為σ 。
線性變換σ的逆σ 也是V的線性變換，稱為σ的逆變換。
當σ是可逆線性變換時，還可以定義σ的負整數次冪σ =(σ 1) ，其中n是非負整數。
這樣，對於可逆線性變換σ來說，
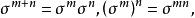可逆線性變換其中m，n可以是任意整數 。
相關性質及證明
定理1 設σ是線性空間V的一個線性變換，稱：
Ker(σ)= { α∈V|σ( α)= 0}
為σ的核；稱：
Im(σ) =σ(V) = {σ( α)| α∈V}
為σ的像(或值域)，Ker(σ)與σ(V)都是V的子空間，且：
dim Ker(σ) + dimσ(V) =n.
證明：容易看出Ker(σ)是V的子空間。現在證明:σ(V)也是V的子空間 。
設 ξ， η是σ( V)的任意兩個向量，那么總存在 α, β∈V，使得 ξ=σ( α)， η=σ( β)，因為σ是V的線性變換，於是對於任意a,b∈F，有：
a ξ+b η=aσ( α) +bσ( β) =σ(a α+b β)∈σ(V)，
這就證明了σ(V)也是V的一個子空間。
設dim Ker(σ) =r,在Ker(σ)中取一個基{ α;..., α}，它可以擴充為V的一個基{ α;..., α, α;..., α}，則：
{σ( α),...,σ( α)}
是像空間σ(V)的一個基。事實上，顯然有：
σ(V)=span{σ( α),.. ,σ( α),σ( α),.. ,σ( α)}.
注意到σ( α)=σ( α)=...=σ( α)= 0，因此：
σ(V) =span{σ( α),...,σ( α)}.
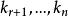可逆線性變換若 ∈F使得kσ( α)+...+kσ( α)= 0，則：
σ(k α+...+k α)= 0,
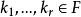可逆線性變換於是，k α+...+k α∈Ker(σ)，因此存在 使得：
k α+...+k α=k α+...+k α
又 α;..., α, α;..., α線性無關，故k=...=k=k=...=k=0，由此可見:σ( α),...,σ( α)線性無關，因此σ( α),...,σ( α)組成σ(V)的一個基，並且dimσ(V) =n-r，故dim Ker(σ) + dimσ(V) =n。
怎樣來判別一個線性變換是否可逆呢?一般來說，一個變換可逆的充分必要條件是這個變換既是單射又是滿射。但是，從定理1出發，可以得到有限維線性空間上的線性變換具有一個很好的性質。
推論1 n維線性空間V.上的線性變換σ是單射的充分必要條件是σ是滿射。
證明顯然，線性變換σ是單射的充分必要條件為Ker(σ)= { 0}，而：
可逆線性變換 可逆線性變換 可逆線性變換Ker(σ)={ 0} dim Ker(σ)=0 dimσ(V)=n σ(V)=V，
因此，線性變換σ是單射的充分必要條件是σ是滿射。
對於線性空間V和W之間的線性映射σ，同樣可以引進核Ker(σ)與σ(V)像的概念，並且可以證明:Ker(σ)是V的子空間，σ(V)是W的子空間
