基本介紹
定義1 劈錐曲面是曲面的一種,給定直線a,平面N內的曲線C,平面M,且a∥N,a和M相交,則滿足下述條件的動直線的軌跡稱為 劈錐曲面(如圖1):
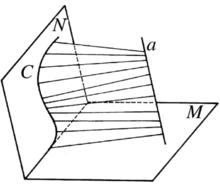 圖1
圖11.動直線平行於平面M;
2.動直線與直線a,曲線C均相交。
其中,定直線a、定曲線C、定平面M分別稱為劈錐曲面的 導向直線、 導向曲線、 導向平面。動直線稱為劈錐曲面的 母線,劈錐曲面被導向直線分成的兩部分,稱為劈錐曲面的 兩葉(圖中只畫出劈錐曲面的一葉);劈錐曲面的每一葉,稱為 半劈錐曲面 。
定義2劈錐曲面是一種曲面,它是由一條平行於已知平面(方向平面)且和已知直線(方向直線)以及已知曲線(方向曲線)相交的直線運動而生成的;當方向曲線為平面曲線時,該方向曲線不得在方向平面上,劈錐曲面是直紋曲面。例如,正螺旋面就是一種劈錐曲面,其方向平面垂直於其軸線,方向曲線——螺旋線,而方向直線——旋轉軸 。
兩種劈錐曲面
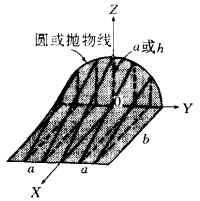 圖2 圖2 | 項點為 劈錐曲面 劈錐曲面 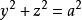 劈錐曲面 劈錐曲面 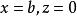 劈錐曲面 劈錐曲面 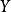 劈錐曲面 劈錐曲面 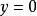 劈錐曲面 劈錐曲面 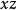 劈錐曲面 劈錐曲面 |
項點為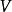 劈錐曲面 劈錐曲面 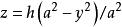 劈錐曲面 劈錐曲面 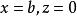 劈錐曲面 劈錐曲面 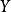 劈錐曲面 劈錐曲面 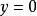 劈錐曲面 劈錐曲面 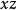 劈錐曲面 劈錐曲面 |
拋物劈錐曲面
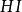 劈錐曲面
劈錐曲面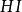 劈錐曲面
劈錐曲面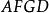 劈錐曲面
劈錐曲面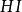 劈錐曲面
劈錐曲面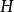 劈錐曲面
劈錐曲面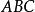 劈錐曲面
劈錐曲面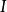 劈錐曲面
劈錐曲面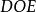 劈錐曲面
劈錐曲面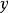 劈錐曲面
劈錐曲面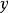 劈錐曲面
劈錐曲面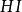 劈錐曲面
劈錐曲面 劈錐曲面
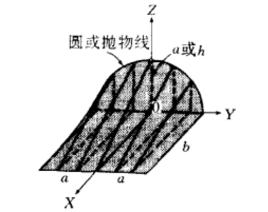
劈錐曲面移動直線形成劈錐曲面。是將保持同參考平面平行,把母線的一端沿著平面曲線移動,另一端沿著直線移動,如圖3所示。平面曲線ABC和直線DOE不但垂直於參考平面 AFGD,而且以DE的中點O為坐標軸原點,則平面曲線的方程必定只是的函式。那么,對任一常數值的母線的方程,可用一常數去乘得到。
因此,可把整個曲面定義為
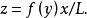 劈錐曲面
劈錐曲面如果平面曲線是拋物線,即
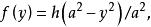 劈錐曲面
劈錐曲面那么這種曲面被定義為 拋物劈錐曲面,可表示為
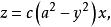 劈錐曲面
劈錐曲面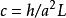 劈錐曲面
劈錐曲面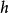 劈錐曲面
劈錐曲面式中,,是拋物線的弦高,如圖3所示 。
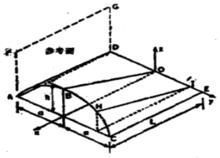 圖3 典型的拋物劈錐曲面
圖3 典型的拋物劈錐曲面圓劈錐曲面
圓劈錐曲面(circular conoid)一種特殊的劈錐曲面,指導向曲線是一個圓的劈錐曲面,圓劈錐曲面的導向曲線稱為導向圓 。