概念
判別損失技術是由費舍(R.A.Fisher)於1936年提出的。它是根據觀察或測量到的若干變數值判斷研究對象如何分類的方法。具體地講,就是已知一定數量案例的一個分組變數和這些案例的一些特徵變數,確定分組變數和特徵變數之間的數量關係,建立判別函式,然後便可以利用這一數量關係對其他已知特徵變數信息,但未知分組類型所屬的案例進行判別分組。
判別損失技術曾經在許多領域得到成功的套用,例如醫學實踐中根據各種化驗結果、疾病症狀、體徵判斷患者患的是什麼疾病;體育選材中根據運動員的體形、運動成績、生理指標、心理素質指標、遺傳因素判斷是否選人運動隊繼續培養;還有動物、植物分類,兒童心理測驗,地理區劃的經濟差異,決策行為預測等。
基本條件
判別損失的基本條件是:分組變數的水平必須大於或等於2,每組案例的規模必須至少在一個以上;各判別變數的測度水平必須在間距測度等級以上,即各判別變數的數據必須為等距或等比數據;各分組的案例在各判別變數的數值上能夠體現差別。判別損失對判別變數有三個基本假設。其一是每一個判別變數不能是其他判別變數的線性組合。否則將無法估計判別函式,或者雖然能夠求解但參數估計的標準誤差很大,以致於參數估計統計性不顯著。其二是各組案例的協方差矩陣相等。在此條件下,可以使用很簡單的公式來計算判別函式和進行顯著性檢驗。其三是各判別變數之間具有多元常態分配,即每個變數對於所有其他變數的固定值有常態分配。
沿用多元回歸模型的稱謂,在判別損失中稱分組變數為因變數,而用以分組的其他特徵變數稱為判別變數(Discriminant Variable)或自變數。
判別損失的基本模型就是判別函式,它表示為分組變數與滿足假設的條件的判別變數的線性函式關係,其數學形式為:
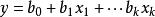 判別損失
判別損失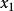 判別損失
判別損失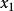 判別損失
判別損失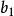 判別損失
判別損失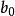 判別損失
判別損失其中,y是判別函式值,又簡稱為判別值(Discriminant Score); 為各判別變數; 為相應的判別係數(Discriminant Coefficient or Weight),表示各判別變數對於判別函式值的影響,其中 是常數項。
判別模型對應的幾何解釋是,各判別變數代表了k維空間,每個案例按其判別變數值稱為這k維空間中的一個點。如果各組案例就其判別變數值有明顯不同,就意味著每一組將會在這一空間的某一部分形成明顯分離的蜂集點群。我們可以計算此領域的中心以概括這個組的位置。中心的位置可以用這個組別中各案例在每個變數上的組平均值作為其坐標值。因為每箇中心代表了所在組的基本位置,我們可以通過研究它們來取得對於這些分組之間差別的理解。這個線性函式應該能夠在把P維空間中的所有點轉化為一維數值之後,既能最大限度地縮小同類中各個樣本點之間的差異,又能最大限度地擴大不同類別中各個樣本點之間的差異,這樣才可能獲得較高的判別效率。在這裡借用了一元方差分析的思想,即依據組問均方差與組內均方差之比最大的原則來進行判別。
基本思想
根據判別中的組數,可以分為兩組判別損失和多組判別損失;
根據判別函式的形式,可以分為線性判別和非線性判別;
根據判別式處理變數的方法不同,可以分為逐步判別、序貫判別等;
根據判別標準不同,可以分為距離判別、Fisher判別、Bayes判別法等。

