定義
冪法主要用於計算矩陣的按模為最大的特徵值和相應的特徵向量 。
基本思想
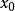冪法求矩陣特徵值若我們求某個n階方陣 A的特徵值和特徵向量，先任取一個初始n維向量 ，構造如下序列：
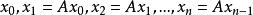冪法求矩陣特徵值(1)
當k增大時,序列的收斂情況與絕對值最大的特徵值有密切關係，分析這一序列的極限,即可求出按模最大的特徵值和特徵向量。
假定矩陣 A有n個線性無關的特徵向量。n個特徵值按模由大到小排列：
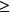冪法求矩陣特徵值 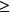冪法求矩陣特徵值 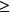冪法求矩陣特徵值│r│ │r│ ... │r│ (2)
其相應的特徵向量為：
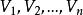冪法求矩陣特徵值(3)
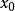冪法求矩陣特徵值它們構成n維空間的一組基。任取的初始向量 由它們的線性組合給出
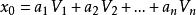冪法求矩陣特徵值(4)
由(1)中的序列可以遞歸得到
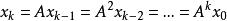冪法求矩陣特徵值(5)
將(4)代入(5)有
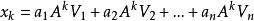冪法求矩陣特徵值(6)
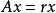冪法求矩陣特徵值將 代入(6)中有
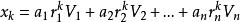冪法求矩陣特徵值(7)
下面按模最大特徵值r是單根的情況討論：
由此公式(7)可寫成
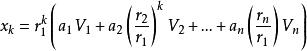冪法求矩陣特徵值(8)
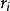冪法求矩陣特徵值
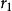冪法求矩陣特徵值
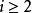冪法求矩陣特徵值若a≠0，由於 / ,( ),故k充分大時，
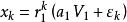冪法求矩陣特徵值
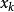冪法求矩陣特徵值
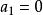冪法求矩陣特徵值其中ε為一可以忽略的小量，這說明 與特徵向量V相差一個常數因子，即使，由於計算過程的捨入誤差，必將引入在方向上的微小分量，這一分量隨著疊代過程的進展而逐漸成為主導，其收斂情況最終也將與相同。
特徵值按下屬方法求得：
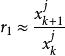冪法求矩陣特徵值(9)
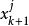冪法求矩陣特徵值
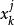冪法求矩陣特徵值
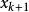冪法求矩陣特徵值 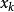冪法求矩陣特徵值其中 ， 分別為 ， 的第j個分量。
計算方法
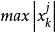冪法求矩陣特徵值
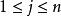冪法求矩陣特徵值 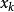冪法求矩陣特徵值
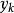冪法求矩陣特徵值
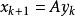冪法求矩陣特徵值實際計算時，為了避免計算過程中出現絕對值過大或過小的數參加運算，通常在每步疊代時，將向量“歸一化”即用的按模最大的分量 , 去除 的各個分量，得到歸一化的向量 ，並令
由此得到下列疊代公式 ：
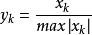冪法求矩陣特徵值 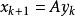冪法求矩陣特徵值
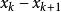冪法求矩陣特徵值當k充分大時，或當║║ <ε 時，
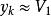冪法求矩陣特徵值
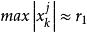冪法求矩陣特徵值，j=1,2,...,n
