簡介
外映射半徑
外映射半徑是複平面上的某個圓盤的半徑。
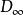 內映射半徑
內映射半徑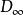 內映射半徑
內映射半徑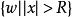 內映射半徑
內映射半徑 內映射半徑
內映射半徑設 E 是複平面 C 上的有界連續統, 是開集 C\E 中那個無界的分支,若共形映射 w=w(z) 將 映成 且在 點的鄰域有展開式
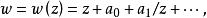 內映射半徑
內映射半徑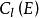 內映射半徑
內映射半徑則稱 R=R(E) 為 E 的外映射半徑。可以證明,R (E) 等於 E 的對數容量 。
定義
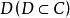 內映射半徑
內映射半徑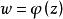 內映射半徑
內映射半徑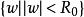 內映射半徑
內映射半徑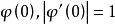 內映射半徑
內映射半徑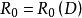 內映射半徑
內映射半徑設 是單連通區域,且其內部含有原點 O。若共形映射 將 D 映成 ,並使 ,則稱 為 D 關於 0 的內映射半徑。
性質
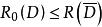 內映射半徑
內映射半徑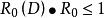 內映射半徑
內映射半徑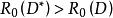 內映射半徑
內映射半徑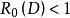 內映射半徑
內映射半徑利用平衡分布的極值性質可證明,當 D 有界時, ,其中等號若且唯若 D 是以原點為中心的開圓;進一步,若把這樣的 D 的外部關於單位圓的反演區域記為 D* ,則 ,等號僅當 D 是單位圓內部時成立,若 ,則 。
共形映射
共形映射是複變函數論的一個分支,它從幾何的觀點來研究複變函數,其通過一個解析函式把一個區域映射到另一個區域進行研究。這個性質可以將一些不規則或者不好用數學公式表達的區域邊界映射成規則的或已成熟的區域邊界。
數學上,一個共形變換(保角變換)是一個保持角度不變的映射。
