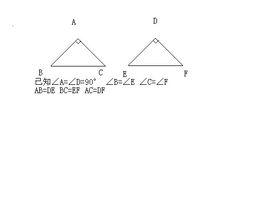
判定一
邊角邊 SAS
在△ABC和△DEF中
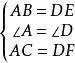 ≌
≌∵
∴△ABC≌△DEF(SAS)
判定二
角邊角 ASA
在△ABC和△DEF中
∵{∠B=∠E
{BC=EF
{∠C=∠F
∴△ABC≌△DEF(ASA)
判定三
角角邊 AAS
在△ABC和△DEF中
∵{∠B=∠E
{∠C=∠F
{AC=DF
∴△ABC≌△DEF(AAS)
角平分線上的點到角的兩邊的距離相等。角平分線
判定四
邊邊邊 SSS
在△ABC和△DEF中
∵{AB=DE
{AC=DF
{BC=EF
∴△ABC≌△DEF(SSS)
三角形的穩定性
判定五
HL垂直全等 ( 直角三角形)
∵AB⊥BC→∠ABC=90°
BD⊥AD→∠BDA=90°
在Rt△ABC和Rt△ABD中 ( Rt三角形,就是直角三角形)
{∠ACB=∠BAD=90°
{AC=BD
{AB=BA
∴△ABC≌△DEF(HL)
截長補短法
截長補短法,是國中數學幾何題中一種輔助線的添加方法,也是把幾何題化難為易的一種思想。截長就是在一條線上截取成兩段,補短就是在一條邊上延長,使其等於一條所求邊。
截長: 1.過某一點作長邊的垂線 2.在長邊上截取一條與某一短邊相同的線段,再證剩下的線段與另一短邊相等。
補短: 1.延長短邊 2.通過旋轉等方式使兩短邊拼合到一起。
例題:
例1:正方形ABCD中,點E在CD上,點F在BC上,∠EAF=45°。 求證:EF=DE+BF 。
證明:延長CD到點G,使得DG=BF,連線AG。
∵ABCD是正方形
∴∠ADG=∠ABF=90°,AD=AB
又∵DG=BF
∴ADG≌ABF(SAS)
∴∠GAD=∠FAB,AG=AF
∵ABCD是正方形
∴∠DAB=90°
=∠DAF+∠FAB
=∠DAF+∠GAD
=∠GAF
∴∠GAE=∠GAF-∠EAF
=90°-45°
=45°
∵∠GAE=∠FAE=45°,AG=AF,AE=AE
∴△EAG≌△EAF(SAS)
∴EF=GE
=GD+DE
=BF+DE
例2:如圖,已知AD∥BC,AB=AD+BC,E是CD的中點,求∠AEB的度數。
解:向AE方向延長AE,交BC的延長線於F。
∵∠5和∠6是對頂角
∴∠5=∠6
∵E是CD的中點
∴DE=EC
∵AD∥BC
∴∠1=∠F
∴△AED≌△CEF(AAS)
∴AD=CF,AE=EF
∴AB=AD+BC
=CF+BC
=BF
∴△ABF是等腰三角形且AF為底邊
又∵AE=EF且點E線上段AF上
∴BE⊥AF
∴∠AEB=90°
例3:如圖,在△ABC中,∠B=2∠C,AD平分∠BAC。求證:AB+BD=AC。
證明:在AC上截取AE=AB,連線DE
∵AD平分∠BAC
∴∠1=∠2
又∵AD=AD,AB=AE
∴△ABD≌△AED(SAS)
∴BD=DE,∠B=∠3
又∵∠B=2∠C
∴∠3=2∠C
又∵∠3=∠4+∠C
∴2∠C=∠4+∠C
即∠C=∠4
∴DE=CE
∴BD=CE
∵AE+EC=AC
∴AB+BD=AC
例4:如圖,AC平分∠DAB,∠ADC+∠B=180°。求證:CD=CB。
證明:在AB上找一點E,使AE=AD,連線CE
∵AC平分∠DAB
∴∠DAC=∠BAC
又∵AE=AD,AC=AC
∴△ACD≌△ACE(SAS)
∴∠ADC=∠AEC,CD=CE
∵∠ADC=∠AEC
∴∠AEC+∠B=∠ADC+∠B=180°
∵∠CEB+∠AEC=180°
∴∠B=∠CEB
∴CE=CB
∴CD=CB