基本性質
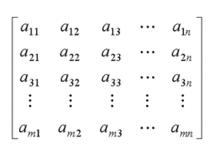 對稱矩陣
對稱矩陣1.對於任何方形矩陣X,X+X 是對稱矩陣。
2.A為方形矩陣是A為對稱矩陣的必要條件。
3.對角矩陣都是對稱矩陣。
4.兩個對稱矩陣的積是對稱矩陣,若且唯若兩者的乘法可交換。兩個實對稱矩陣乘法可交換若且唯若兩者的特徵空間相同。
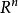 對稱矩陣
對稱矩陣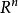 對稱矩陣
對稱矩陣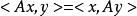 對稱矩陣
對稱矩陣5.用<,>表示 上的內積。n×n的實矩陣A是對稱的,若且唯若對於所有X, Y∈ , 。
6.任何方形矩陣X,如果它的元素屬於一個特徵值不為2的域(例如實數),可以用剛好一種方法寫成一個對稱矩陣和一個斜對稱矩陣之和:
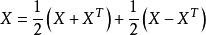 對稱矩陣
對稱矩陣7.每個實方形矩陣都可寫作兩個實對稱矩陣的積,每個複方形矩陣都可寫作兩個復對稱矩陣的積。
8.若對稱矩陣A的每個元素均為實數,A是Symmetric矩陣。
9.一個矩陣同時為對稱矩陣及斜對稱矩陣若且唯若所有元素都是零的時候成立。
10.如果X是對稱矩陣,那么對於任意的矩陣A,AXA 也是對稱矩陣。
11.n階實對稱矩陣,是n維歐式空間V(R)的對稱變換在單位正交基下所對應的矩陣。
矩陣轉置
把一個m×n矩陣的行,列互換得到的n×m矩陣,稱為A的轉置矩陣,記為A'或A 。
矩陣轉置的運算律(即性質):
1.(A')'=A
2.(A+B)'=A'+B'
3.(kA)'=kA'(k為實數)
4.(AB)'=B'A'
若矩陣A滿足條件A=A',則稱A為對稱矩陣。由定義知對稱矩陣一定是方陣,而且位於主對角線對稱位置上的元素必對應相等,即a=a對任意i,j都成立。
套用
1.對稱矩陣
(1)對稱矩陣
在一個n階方陣A中,若元素滿足下述性質:
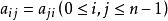 對稱矩陣
對稱矩陣則稱A為對稱矩陣。
(2)對稱矩陣的壓縮存儲
對稱矩陣中的元素關於主對角線對稱,故只要存儲矩陣中上三角或下三角中的元素,讓每兩個對稱的元素共享一個存儲空間。這樣,能節約近一半的存儲空間。
①按行優先順序存儲主對角線(包括對角線)以下的元素
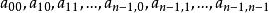 對稱矩陣
對稱矩陣即按 次序存放在一個向量sa[0...n(n+1)/2-1]中(下三角矩陣中,元素總數為n(n+1)/2)。
其中:
sa[0]=a
sa[1]=a
……
sa[n(n+1)/2-1]=a
②元素aij的存放位置
a元素前有i行(從第0行到第i-1行),一共有:
1+2+…+i=i×(i+1)/2個元素。
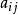 對稱矩陣
對稱矩陣在第i行上, 之前恰有j個元素,即aa…,a,因此有:
sa[i×(i+1)/2+j]=a
③a和sa[k]之間的對應關係:
若i≥j,k=i×(i+1)/2+j0≤k<n(n+1)/2
若i<j,k=j×(j+1)/2+i0≤k<n(n+1)/2
令I=max(i,j),J=min(i,j),則k和i,j的對應關係可統一為:
k=i×(i+1)/2+j0≤k<n(n+1)/2
(3)對稱矩陣的地址計算公式
LOC(a)=LOC(sa[k])
=LOC(sa[0])+k×d=LOC(sa[0])+[I×(I+1)/2+J]×d
通過下標變換公式,能立即找到矩陣元素aij在其壓縮存儲表示sa中的對應位置k。因此是隨機存取結構。
【例】a和a均存儲在sa[4]中,這是因為
k=I×(I+1)/2+J=2×(2+1)/2+1=4

