介紹
我們可以看到,如果一個二叉排序樹節點插入的順序是隨機的,這樣我們得到的二叉排序樹大多數情況下是平衡的,即使存在一些極端情況,但是這種情況發生的機率很小,所以我們可以這樣建立一顆二叉排序樹,而不必要像AVL那樣旋轉,可以證明隨機順序建立的二叉排序樹在期望高度是,但是某些時候我們並不能得知所有的帶插入節點,打亂以後再插入。所以我們需要一種規則來實現這種想法,並且不必要所有節點。也就是說節點是順序輸入的,我們實現這一點可以用Treap。Treap=Tree+Heap
Treap是一棵二叉排序樹,它的左子樹和右子樹分別是一個Treap,和一般的二叉排序樹不同的是,Treap紀錄一個額外的數據,就是優先權。Treap在以關鍵碼構成二叉排序樹的同時,還滿足堆的性質(在這裡我們假設節點的優先權大於該節點的孩子的優先權)。但是這裡要注意的是Treap和二叉堆有一點不同,就是二叉堆必須是完全二叉樹,而Treap可以並不一定是。
操作
Treap維護堆性質的方法用到了旋轉,這裡先簡單地介紹一下。Treap只需要兩種旋轉,這樣編程複雜度比Splay等就要小一些,這正是Treap的特色之一。旋轉是這樣的:
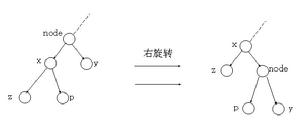
插入
給節點隨機分配一個優先權,先和二叉排序樹的插入一樣,先把要插入的點插入到一個葉子上,然後跟維護堆一樣,如果當前節點的優先權比根大就旋轉,如果當前節點是跟的左兒子就右旋如果當前節點是跟個右兒子就左旋。
我們如果把插入寫成遞歸形式的話,只需要在遞歸調用完成後判斷是否滿足堆性質,如果不滿足就旋轉,實現非常容易。
由於旋轉是的,最多進行h次(h是樹的高度),插入的複雜度是log( n )的,在期望情況下,所以它的期望複雜度是 O( log( N ) );
插入代碼:
void insert(int &x,int y)
{
if (x==0)
{
x=++size;
e[x].l=0;e[x].r=0;e[x].a=y;e[x].b=rand()*rand();
e[x].ll=0;e[x].rr=0;// .ll記錄了左兒子個數. .RR記錄了右兒子個數 .l記錄了左兒子編號. .R記錄了右兒子編號。
return;
}
if (y>e[x].a)
{
insert(e[x].r,y);
e[x].rr++;
if (e[x].b>e[e[x].r].b) right(x);
return;
}
if (y<=e[x].a)
{
insert(e[x].l,y);
e[x].ll++;
if(e[x].b>e[e[x].l].b) left(x);
return;
}
}
刪除
有了旋轉的操作之後,Treap的刪除比二叉排序樹還要簡單。因為Treap滿足堆性質,所以我們只需要把要刪除的節點旋轉到葉節點上,然後直接刪除就可以了。具體的方法就是每次找到優先權最大的兒子,向與其相反的方向旋轉,直到那個節點被旋轉到了葉節點,然後直接刪除。刪除最多進行log( n )次旋轉,期望複雜度是log( n )。
void Delete(int &x,int y)
{
if (e[x].a==y)
{
if (e[x].l==0||e[x].r==0)
{
if (e[x].l==0)
{x=e[x].r;return;}
if (e[x].r==0)
{x=e[x].l;return;}
}
if (e[e[x].l].b
{
left(x);
e[x].rr--;
Delete(e[x].r,y);
}else
{
right(x);
e[x].ll--;
Delete1(e[x].l,y);
}
}
else
{
if (e[x].a>y) { e[x].ll--;Delete1(e[x].l,y);}
if (e[x].a<=y) { e[x].rr--;Delete1(e[x].r,y);}
}
}
第二種刪除方法:為保證效率,可以用普通二叉查找樹的刪除方法,找到節點的中序前綴,然後替換,刪除,並使用非遞歸。雖然時間複雜度仍為log級別,但常數因子小了很多。
Pascal代碼:
procedure del(x:longint);
var
now,MinMax,p:point;
begin
now:=root; //root為根指針
null^.x:=x;
while now^.x <> x do
begin
p:=now;
if now^.x > x then
now:=now^.l
else
now:=now^.r;
end;
if now = null then // 沒找到X
exit;
if now^.l <> null then // 左子樹不為空,往左找
begin
MinMax:=now^.l;
p:=now;
while MinMax^.r <> null do
begin
p:=MinMax;
MinMax:=MinMax^.r;
end;
now^.x:=MinMax^.x;
if p <> now then
p^.r:=MinMax^.l
else
p^.l:=MinMax^.l;
dispose(MinMax);
end
else
if now^.r <> null then // 右子樹不為空,往右找
begin
MinMax:=now^.r;
p:=now;
while MinMax^.l <> null do
begin
p:=MinMax;
MinMax:=MinMax^.l;
end;
now^.x:=MinMax^.x;
if p <> now then
p^.l:=MinMax^.r
else
p^.r:=MinMax^.r;
dispose(MinMax);
end
else // X本身是葉子
begin
if p^.x > x then
p^.l:=null
else
p^.r:=null;
dispose(now);
end;
end;
查找
和一般的二叉排序樹一樣,但是由於Treap的隨機化結構,可以證明Treap中查找的期望複雜度是log( n )。分離
要把一個Treap按大小分成兩個Treap,只要在需要分開的位置加一個虛擬節點,然後旋至根節點刪除,左右兩個子樹就是得出的兩個Treap了。根據二叉排序樹的性質,這時左子樹的所有節點都小於右子樹的節點。時間相當於一次插入操作的複雜度,也就是 log( n )
合併
合併是指把兩個Treap合併成一個Treap,其中第一個Treap的所有節點都必須小於或等於第二個Treap中的所有節點,也就是分離的結果所要滿足的條件。合併的過程和分離相反,只要加一個虛擬的根,把兩棵樹分別作為左右子樹,然後把根刪除就可以了。時間複雜度和刪除一樣,也是期望
旋轉
旋轉就是把random出來的值進行維護堆得性質的操作.因為BST得特殊性質,所以在旋轉時,還要維護BST的性質。void right(int &x)
{
int j=e[x].r;
e[x].r=e[j].l;
e[x].rr=e[j].ll;
e[j].l=x;
e[j].ll=e[x].ll+e[j].ll+1;
x=j;
}
void left(int &x)
{
int j=e[x].l;
e[x].l=e[j].r;
e[x].ll=e[j].rr;
e[j].r=x;
e[j].rr=e[x].rr+e[j].rr+1;
x=j;
}
算法分析
首先我們注意到二叉排序樹有一個特性,就是每個子樹的形態在優先權唯一確定的情況下都是唯一的,不受其他因素影響,也就是說,左子樹的形態與樹中大於根節點的值無關,右子樹亦然。這是因為Treap滿足堆的性質,Treap的根節點是優先權最大的那個節點,考慮它的左子樹,樹根也是子樹裡面最大的一點,右子樹亦然。所以Treap相當於先把所有節點按照優先權排序,然後插入,實質上就相當於以隨機順序建立的二叉排序樹,只不過它並不需要一次讀入所有數據,可以一個一個地插入。而當這個隨機順序確定的時候,這個樹是唯一的。
因此在給定優先權的情況下,只要是用符合要求的操作,通過任何方式得出的Treap都是一樣的,所以不改變優先權的情況下,特殊的操作不會造成Treap結構的退化。而改變優先權可能會使Treap變得不夠隨機以致退化。
證明隨機建立二叉排序樹的大家可以參見CLRS P265 12.4 Randomly built binary search trees,這裡略去。
如果有我們就證明了,Treap插入的期望複雜度是
Treap的其它操作的期望複雜度同樣是
優點與缺點
優點
實現簡單,效率高,性價比很高
缺點
引用
外部連結
一個Treap的演示(做得太好了,不說了大家看看就知道了...)
Randomized Search Trees(pdf), 有對Treap和它的加權形式的詳盡介紹以及複雜度的嚴格證明
