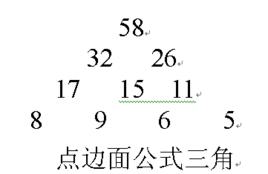
定義
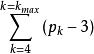 點邊面公式
點邊面公式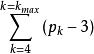 點邊面公式
點邊面公式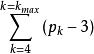 點邊面公式
點邊面公式假設空間中有n個點,其中沒有四個或其以上的點在一個平面 中,那么其邊 的數量為l=n*(n-1)/2,可見邊的數量為l=3*n-6,平面的數量s=n*(n-1)(n-2)/6,由可見邊構成的平面的數量為s=3*n-8,其中隱藏面 數量n-4,如果有多個點在一個平面 上,那么可見邊數量l=3n-6-,可見面數量s=2n-4-,其中n為點的總個數,為可見面中共麵點超過3個點的點的數量和,其中k為四點以上共面的可見面。
舉例:
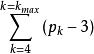 點邊面公式
點邊面公式1.一個四邊形和一個五邊形在空間中,沒有其它任何四點以上的面共面,它的可見邊數量l=3×9-6-(2+1)=18,可見面數量s=2×9-4-(2+1)=11,其中n=9,=(4-3)+(5-3)=2+1=3。
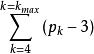 點邊面公式
點邊面公式2.立方體,它的可見邊數量l=3×8-6-(1+1+1+1+1+1)=12,可見面數量s=2×8-4-(1+1+1+1+1+1)=6,其中n=8,=(4-3)+(4-3)+(4-3)+(4-3)+(4-3)+(4-3)=1+1+1+1+1+1=6。