證明
由三角形面積公式S=(1/2)×a×b×sinC推導出:
 共角三角形
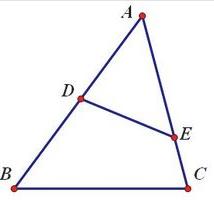
共角三角形若△ABC和△ADE中,
∠BAC=∠DAE 或∠BAC+∠DAE=180°,
則S△ABC÷S△ADE=(AB×AC)÷(AD×AE)
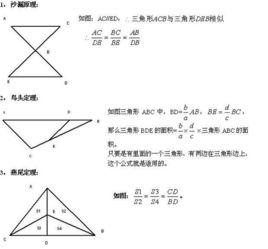
鳥頭定理是若兩三角形有一組對應角相等或互補,則它們的面積比等於對應角兩邊乘積的比。
證明
由三角形面積公式S=(1/2)×a×b×sinC推導出:
 共角三角形
共角三角形若△ABC和△ADE中,
∠BAC=∠DAE 或∠BAC+∠DAE=180°,
則S△ABC÷S△ADE=(AB×AC)÷(AD×AE)
