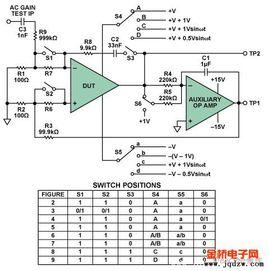
定義
高增益觀測器在如下形式的非線性系統:
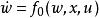 高增益觀測器
高增益觀測器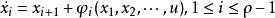 高增益觀測器
高增益觀測器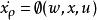 高增益觀測器
高增益觀測器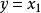 高增益觀測器
高增益觀測器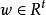 高增益觀測器
高增益觀測器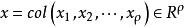 高增益觀測器
高增益觀測器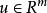 高增益觀測器
高增益觀測器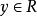 高增益觀測器
高增益觀測器其中, 和 為狀態向量, 為輸入, 為可量測的輸出。
可以看出標稱模型是該系統的一種特殊情況,
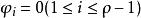 高增益觀測器
高增益觀測器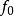 高增益觀測器
高增益觀測器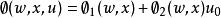 高增益觀測器
高增益觀測器即其中 , 和u無關,且 。
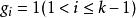 高增益觀測器
高增益觀測器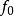 高增益觀測器
高增益觀測器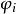 高增益觀測器
高增益觀測器 高增益觀測器
高增益觀測器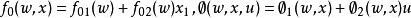 高增益觀測器
高增益觀測器更進一步,嚴格反饋型也是它的一種特殊情況,其中 , 和 與 無關,並具有 的形式。
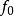 高增益觀測器
高增益觀測器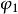 高增益觀測器
高增益觀測器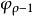 高增益觀測器
高增益觀測器 高增益觀測器
高增益觀測器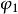 高增益觀測器
高增益觀測器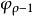 高增益觀測器
高增益觀測器 高增益觀測器
高增益觀測器假設在研究的區域內, , ,…, 和 對其變數是局部Lipschitz的, ,…, 關於x對 是一致Lipschitz的,即
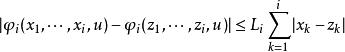 高增益觀測器
高增益觀測器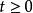 高增益觀測器
高增益觀測器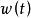 高增益觀測器
高增益觀測器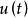 高增益觀測器
高增益觀測器進一步,我們假設對於所有 , 和 都是有界的。
用於觀測z的部分狀態觀測器可設計成
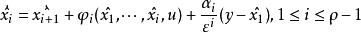 高增益觀測器
高增益觀測器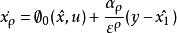 高增益觀測器
高增益觀測器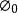 高增益觀測器
高增益觀測器 高增益觀測器
高增益觀測器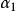 高增益觀測器
高增益觀測器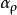 高增益觀測器
高增益觀測器其中, 關於x對u是一致的Lipschitz函式, 是充分小的正常數,選擇 ,…, ,以使
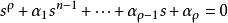 高增益觀測器
高增益觀測器 高增益觀測器
高增益觀測器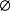 高增益觀測器
高增益觀測器的所有根具有負實部,部分狀態觀測器式中的 是 的標稱型。假設
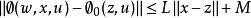 高增益觀測器
高增益觀測器因為
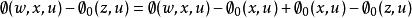 高增益觀測器
高增益觀測器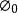 高增益觀測器
高增益觀測器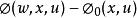 高增益觀測器
高增益觀測器且 是Lipschitz的,所以上式就是要求建模 誤差有界。
引理
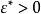 高增益觀測器
高增益觀測器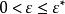 高增益觀測器
高增益觀測器在上述條件下,存在 ,使得對於 。,高增益觀測器式的估計誤差
滿足
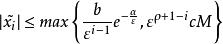 高增益觀測器
高增益觀測器證明:定義標量估計誤差
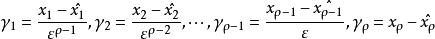 高增益觀測器
高增益觀測器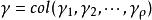 高增益觀測器
高增益觀測器可以證明 滿足方程
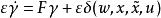 高增益觀測器
高增益觀測器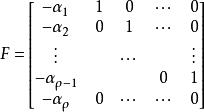 高增益觀測器
高增益觀測器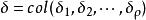 高增益觀測器
高增益觀測器 高增益觀測器
高增益觀測器, 和
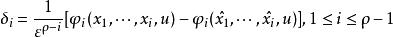 高增益觀測器
高增益觀測器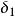 高增益觀測器
高增益觀測器 高增益觀測器
高增益觀測器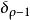 高增益觀測器
高增益觀測器因為F的特徵方程是式是Hurwitz矩陣。根據上式得, , , 滿足
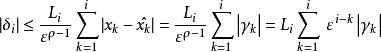 高增益觀測器
高增益觀測器由此可得
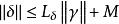 高增益觀測器
高增益觀測器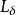 高增益觀測器
高增益觀測器 高增益觀測器
高增益觀測器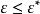 高增益觀測器
高增益觀測器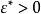 高增益觀測器
高增益觀測器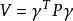 高增益觀測器
高增益觀測器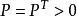 高增益觀測器
高增益觀測器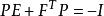 高增益觀測器
高增益觀測器其中, 和 無關,這裡的 ,而 是任意給定的。取 ,其中 為Lyapunov方程 的解,則
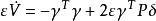 高增益觀測器
高增益觀測器由上式可得 ‘
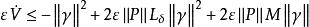 高增益觀測器
高增益觀測器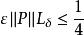 高增益觀測器
高增益觀測器選取,可得
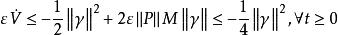 高增益觀測器
高增益觀測器由定理可知
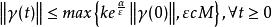 高增益觀測器
高增益觀測器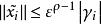 高增益觀測器
高增益觀測器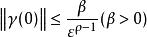 高增益觀測器
高增益觀測器其中,a、c和k為正常數。由上式可得,如果和,定理得證。