昨線性微分代數系統的研究背景
隨著工業系統規模的擴大以及科學研究的深入，非線性複雜系統受到越來越多的關注.，並逐漸成為國際控制界的一個熱點研究方向甲很多非線性複雜系統，包括電力系統和複雜的電網路、受限機械系統與機器人系統、化工過程、人口模型以及社會經濟系統等，都是由若千動態子系統和靜態子系統通過強烈禍合構成的，各動態子系統除了分別具有各自的動態特性外，還與其他子系統存在複雜的聯繫和制約。由子動態子系統的特性一般用微分方程來描述，而靜態子系統的特性以及各子系統之間的聯繫和制約用代數方程來描述，這些系統的數學模型需要表示為由微分方程和代數方程共同組成的混合模型
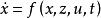非線性微分代數系統
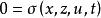非線性微分代數系統
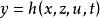非線性微分代數系統在相關文獻中，微分代數系統還被稱為受限系統、奇異系統、廣義系統、描述變數系統或半狀態系統等。這些稱謂從不同側面反映了微分代數系統模型的特點，表達了系統的複雜性。
微分代數系統是一種更具一般性的系統模型，它是在系統建模過程直接得到的，其中的變數往往具有明確的物理意義。在對微分代數系統進行研究時，最直接的想法是通過模型化簡將其轉化為微分方程系統，遺憾的是，對非線性微分代數系統，模型化簡併不總能實現即使在特定條件下能夠把微分代數系統化為微分方程系統，也會造成具有實際意義的變數的缺失，不利於對系統進行全面的分析和有效的控制。
例如，在對電力系統穩定性分析和控制的研究中發現，雖然可以在恆阻杭負荷等假設下，通過消去母線電壓變數而將電力系統模型化為微分方程系統，但是由於母線電壓變數是衡量系統電壓穩定性的主要變數，基於化簡模型將無法有效分析系統電壓穩定性.隨著對電力系統穩定性問題認識的深人，人們發現電壓穩定對電力系統的安全穩定運行起著關鍵作用，基於微分代數模型的電力系統研究日益受到重視。
大量研究結果表明，由於代數約束方程的存在，微分代數系統會呈現出很多微分方程系統所不具有的現象和特點，例如在電路網路中觀察到的脈衝和跳變現象，微分代數系統從低指數向高指數演變而產生的奇異誘導分岔現象等。基於微分代數系統模型進行分析與控制研究可以更加深刻地揭示這些現象的本質。
從系統模型結構特點來看，微分代數系統能夠反映實際系統中大量存在的分層現象：底層是系統的動態特性，上層是系統的靜態特性和管理特性，所以微分代數系統理論也許是處理具有多級、多目標、多維數和多層次的大規模複雜系統的一個有力工具。
綜上所述，現實世界已為微分代數系統的研究提供了深刻的物理背景和廣泛的套用前景。目前，雖然線性微分代數系統的研究已經較為系統，但非線性微分代數系統的研究卻尚末充分展開，特別是在系統分析和控制中未能充分利用系統內在的結構特點。
非線性微分代數系統的特點
由於代數約束方程以及隱動態代數變數的存在，非線性微分代數系統具有許多不同於微分方程系統的特徵，主要包括:
奇異性
奇異性是微分代數系統最重要的特性，可以用微分指數來表征所謂微分指數就是通過系統擴張把微分代數系統化為等價的微分方程系統所需要的最少求導次數。微分方程系統是指數為零的微分代數系統。目前的研究結果表明指數1微分代數系統具有和微分方程系統類似的性質，而指數大於1的微分代數系統(高指數系統)和微分方程系統有明顯差別，其動態行為也更加複雜。
行為高度複雜性
非線性微分代數系統解的情況非常複雜，具有無解、多解、唯一解等多種情況。首先，在求解過程中，系統初始條件的確定不再是一個平凡間題，必須滿足所謂的一致初始條件，該條件是根據約束方程或對其多次求導並經過複雜計算得到的，求導次數的多少與微分代數系統的奇異性直接相關，如果一致初始條件不能得到滿足，可能會導致系統無解，或者迫使系統中部分狀態發生跳變。另外，如果參數變化導致微分代數系統在運行過程由低指數向高指數轉化，會發生由於奇異性造成的分岔現象，出現更為複雜的動態行為。
非因果性
通俗地講，因果性是系統狀態變數和輸出變數依賴於當前和以前時刻的輸入量值，而非因果性是指系統中各變數不僅依賴於當前和以前時刻的輸人變數，還依賴以後時刻的輸入量值.對高指數微分代數系統，如果代數約束方程依賴於輸人量，則系統某些狀態變數回響中會出現輸入量的微分，導致非因果關係的產生。
不具有全局穩定性
微分代數系統在狀態空間中通過奇異面分割成多個連通的分支，各連通的分支在交接的地方是奇異的，而在每個連通分支內部則是非奇異的，有各自的吸引域、穩定域、不穩定域以及穩定極限集等，所以非線性微分代數系統不具備全局穩定性。
和其他系統的區別
為了進一步說明非線性微分代數系統的特點，下面將其與其他幾種重要的系統模型進行比較。
微分代數系統與微分方程系統
從模型特徵上看，隱式形式的非線性微分代數系統是微分方程系統和微分代數系統的通用表達形式。
微分代數系統又褲稱為流形上的微分方程系統，兩者之間的關係是顯然的.但是，微分代數系統無論在定性特性還是在結構上與微分方程系統都有本質的區別，不能簡單地將微分代數系統看成是微分方程系統的隱描述在對微分代數系統進行研究時，不僅要考慮其動態特性，還要考慮由於代數方程所確定的系統的靜態特性。
微分代數系統與非完整系統
微分代數系統和非完整系統都是受到約束作用的微分方程系統，微分代數系統是受到代數方程約束的系統，這類約束可以看作幾何約束，理論上能夠通過消去冗餘坐標將系統化為不受約束的系統。非完整系統是系統中某些變數及其導數受到代數約束的一類微分方程系統，這種約束是速度約束，不能通過積分化為幾何約束。
微分代數系統與奇異攝動系統
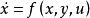非線性微分代數系統奇異攝動系統模型為
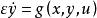非線性微分代數系統其中ε為奇異攝動量，當ε=O時，奇異攝動系統就是微分代數系統，所以微分代數系統可以用來表示奇異攝動系統慢動態的特性。反過來，在微分代數系統的分析中，也可以以充分小的奇異攝動量二下的奇異攝動系統近似代替微分方程系統。但是，奇異攝動系統和微分方程系統之間也存在本質上的區別：對奇異攝動系統，ε符號的不同將直接影響系統的動態行為，而無論g( x，y，u)的符號如何，微分代數系統中代數約束流形可以保持不變；另外，奇異攝動系統可以具有全局穩定性和全局動態，而微分代數系統僅具有局部穩定性和局部動態。
非線性微分代數系統的穩定性分析
微分代數系統中代數變數動態是由狀態變鼻和代數方程(對高指數非線性微分代數系統，還包括代數方程的導數)隱式決定的.，所以無法直接得到Lyapunov函式的導數，為系統穩定性分析帶來了困難.綜觀目前的研究結果，非線性微分代數系統的主要穩定性分析方法可以歸為以下幾種：
(1)把微分代數系統局部歸結為流形上的微分方程，即受限微分方程，發展出平行於常微分方程的理論.
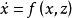非線性微分代數系統具體地，對指數1自治非線性微分代數系統
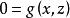非線性微分代數系統基於上述變換，陳伯山等給出了非線性微分代數系統的一般形式的LyaPunov函式，討論了系統平凡解的穩定性判據和吸引域。基於非線性系統的穩定性分析結果分別研究了系統鎮定和觀測器設計問題，劉永清等則給出了非線性微分代數系統穩定以及漸近穩定的條件。
(2)針對微分代數系統的特定形式，推廣穩定性的概念，構造特殊的函式，研究各種特殊的穩定性問題，提出了一些適用於隱式非線性微分代數系統的Lyapunov穩定性概念。利用這些概念，證明了指數1非線性微分代數系統零解的穩定性和漸近穩定，得出了指數1微分代數系統零解穩定性的一些判據，並利用這些結果解決了電力系統的一些穩定性問題等。在假設系統存在唯一無脈衝解的條件下，研究了非線性微分代數系統的穩定性分析問題，給出了微分代數系統穩定性及漸近穩定性的定義。由於公代表系統中慢動態量，這種分析方法可稱為慢子系統分析方法。
(3)用奇異攝動系統近似代替微分代數系統，
這種近似方法在電力系統穩定性分析中得到了大量套用，但是微分代數系統和奇異攝動系統模型存在較大區別，而且奇異攝動的方式和奇異攝動的大小對系統暫態過程都有較大影響。
優點
在電力系統分析中採用微分代數模型具有以下優點:
(1)微分代數模型能夠更加準確地表示電力系統中元件的特性，包括發電機動態特性、負荷特睦等;
(2)在系統數值仿真中可以採用疏鬆矩陣技術，便於提高系統線上分析的快速性;
(3)能夠更精確地構造系統的能量函式，從而更準確地分析系統的穩定性，
估計系統的穩定域;
(4)能夠對負荷母線電壓變數進行分析，從而對目前受到越來越多關注的電壓穩定問題以及電能質量問題給予更加精確和直觀的描述和分析.
在基於微分代數模型的電力系統分析研究中，穩定性分析是人們長期關注的研究課題，在電力系統穩定性問題研究的早期，人們認為大擾動下系統的暫態穩定性問題主要是暫態功角穩定性問題，並主要基於經典模型通過搖擺曲線來判斷系統穩定性(經典模型是電力系統非線性微分代數系統模型在恆阻抗負荷假設下，通過消去負荷母線電壓變數而得到的)，七十年代後期以來，國際上多次發生的由於電壓崩潰引起的大面積停電事故迫使人們開始關注電壓穩定問題，即負荷母線電壓的穩定性問題，並使得穩定性研究從單純的功角穩定性發展到綜合考慮功角和電壓穩定性。具體地，在系統功角穩定的條件下，如果在搖擺過程中若系統節點電壓接近極限或者過負荷，或者節點電壓低於某一極限值，那么即使從發電機搖擺曲線上看系統是穩定的，整個系統也暫態不穩定.
電力系統電壓穩定性分析主要包括靜態分析和動態分析。在電壓穩定性研究的初期人們關注的是靜態電壓穩定性問題甲基於潮流方程或者假設發電機後電勢恆定的擴展潮流方程的分析方法是靜態電壓穩定性分析的主要研究方法，並將網路傳輸極限功率時系統的運行狀態作為靜態電壓穩定極限，靜態分析仍是目前電壓穩定研究工作中最富成果的方向之一。
隨著電壓研究的深人，人們逐漸認識到電壓穩定本質上是一個動態問題，系統中諸多動態因素，如OLTC動態、發電機及其勵磁控制系統、負荷動態特性、無功補償設備等均對電壓穩定起著重要作用，從而開始用動態觀點探討電壓穩定的機理，提出了基於微分代數方程的研究方法，包括小擾動分析方法以及暫態分析方法。小擾動分析方法是將描述電力系統的微分代數系統在運行點附近線性化，消去代數約束後形成系統矩陣，然後通過該矩陣的特徵值和特徵向量來分析系統的穩定性。由於動態負荷、發電機及勵磁控制系統、FACTS裝置等均是動態元件，其暫態行為也可能導致電壓不穩，同時大擾動情況會導致電力系統運行狀態較大地偏離正常運行點，故暫態穩定分析也引起了人們的關注，由於暫態穩定分析的複雜性，目前的研究集中於動態負荷，特別是電動機負荷特性對電壓穩定的影響。
非線性微分代數系統控制
目前文獻中涉及的非線性微分代數系統控制問題很多，包括鎮定、跟蹤、解藕、觀測器設計以及魯棒、最佳化和自適應控制等，所採用的方法主要有反饋線性化方法、LyaPunov方法以及變結構方法等，這些方法都是非線性系統控制方法在微分代數系統中的推廣。
基於反饋線性化的非線性微分代數系統控制研究
反饋線性化是非線性系統中一種重要的綜合方法，包括精確反饋線性化方法，即微分幾何方法直接反饋線性化以及逆系統方法等以及多種近似反饋線性化方法。對完成線性化後的系統，除了可以完成系統鎮定之外，還可以通過分層控制策略或者分步設計方法完成魯棒、最佳化以及自適應控制器的設計，很多學者將反饋線性化方法推廣到非線性微分代數系統，並在反饋線性化的基礎上完成了鎮定、解藕、魯棒以及自適應控制等。
從目前非線性微分代數系統控制問題的研究結果來看，基於反饋線性化方法的研究占據著主導位置.通過將非線性微分代數系統化為等價的微分方程系統，將微分幾何方法直接套用於系統的反饋線性化，完成了系統鎮定，將受限動態算法和零動態算法推廣到仿射非線性系統，通過坐標變換完成了系統的輸人輸出線性化，並基於線性化系統設計了鎮定控制器；同時，反饋線性化方法套用於微分代數系統的解禍控制和跟蹤控制。wang等則推廣了微分幾何方法中李導數和李括弧的概念，提出了M導數和M括弧的概念，完成了非線性微分代數系統的反饋線性化，通過將代數約束表示為線性約束，實現微分幾何方法在非線性微分代數系統反饋線性化研究中的推廣。對多輸人多輸出系統，反饋線性化後的系統往往包含有零動態，而且零動態系統的穩定性決定系統的內部穩定性，研究非線性微分代數系統的零動態問題對考慮外部擾動和參數不確定性的非線性微分代數系統，採用反饋線性化和自適應控制方法給出了自適應控制器的設計方法，為了解決狀態變數不能直接測量問題，研究基於觀測器的反饋線性化問題，作為反饋線性化方法的套用，受限機械系統、機器人系統以及電力系統中若干控制問題得到了研究。
反饋線性化方法首先通過坐標變換和狀態反饋消去系統中非線性項，從而將系統轉換為線性系統，然後採用成熟的線性系統理論設計控制器使閉環系統具有期望的性能。但是，反饋線性化方法也有其內在缺陷:採用這種控制方法可能會消去系統中原有的對穩定性和動態性能具有良好作用的非線性環節，增加反饋控制的力度，帶來噪聲放大等負面影響。
基於LyaPunov方法的非線性微分代數系統控制研究
LyaPunov方法是適於任何系統類型的基本的分析和綜合方法，但由於微分代數系統中代數變數是隱式決定的，同系統穩定性分析一樣，必須藉助適當的手段才能完成系統綜合。
通過將非線性微分代數系統化為流形上的微分方程系統，基於LyaPunov方法設計系統的反饋鎮定器，給出一種鎮定控制器存在的條件，但沒有給出控制器的具體構造方法。Lyapunov函式滿足對合條件時，wang Hesheng等採用LyaPunov方法研究了非線性微分代數系統凡控制問題，分別給出了狀態反饋和輸出反饋時坑問題可解的條件，並基於微分對策和耗散不等式，構造了一族輸出反饋凡控制器，該結論是LyaPunov和KangI以及非線性系統的相關結果在微分代數系統中的推廣，特別需要指出的是，Wang等將微分代數的幾干擾抑制問題歸結為兩個不等式的非負定解的存在性問題，該結論是仿射非線性系統有關結果在微分代數系統中的推廣。
其他控制方法及控制問題
由於變結構方法的強魯棒性在很多領域得到了套用，溫香彩、劉永清等將變結構方法套用於微分代數系統的控制，取得了良好的控制效果。等對一類非線性微分代數系統提出一種二次型LyaPunov函式，並採用凸最佳化方法將一類非線性微分代數系統的鎮定問題轉化為不等式的求解問題。將增益調節控制方法套用於非線性微分代數系統的魯棒控制，他對一類特殊的非線性微分代數系統設計了控制器，這類系統的系統矩陣仿射依賴於一些有界的非線性變數，通過將擴展的有界實理推廣到微分代數系統，並最終將系統的戈控制器設計問題歸結求解問題。
此外，作為非線性微分代數系統中特有的控制間題，反饋正則化問題也得到了研究。所謂反饋正則化就是通過反饋控制將高指數微分代數系統化為指數1微分代數系統，同時達到消去系統中脈衝行為的目的。將零動態方法套用於非線性微分代數系統，給出了系統實現正則化的算法運用一般意義上的中心流形定理討論了一類非線性微分代數系統的輸出正則化問題，並通過設計控制律使得閉環系統能夠漸近跟蹤一類參考輸入。
