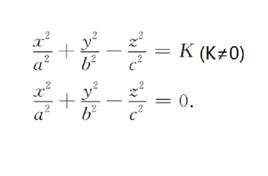基本介紹
雙曲面(hyperboloid(surface))是指在通過主軸的平面上，截痕是雙曲線，而在與主軸垂直的平面上的截痕是橢圓的二次曲面。它分為單葉雙曲面和雙葉雙曲面，它們都關於三個相互垂直的平面中每一個平面對稱。
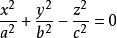雙曲面漸近錐面
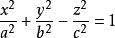雙曲面漸近錐面
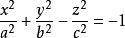雙曲面漸近錐面在平面幾何中，雙曲線有漸近線，相類似地，雙曲面也有漸近錐面。二次錐面是單葉雙曲面和雙葉雙曲面的漸近錐面 。
二次錐面是雙曲面的漸近錐面
現在我們來考慮單葉雙曲面(1)和雙葉雙曲面(2)與二次錐面(3)。
單葉雙曲面
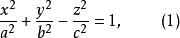雙曲面漸近錐面雙葉雙曲面
雙曲面漸近錐面二次錐面
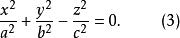雙曲面漸近錐面當它們有相同的正數a，b，c時，則它們有密切的關係。
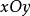雙曲面漸近錐面
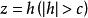雙曲面漸近錐面用平行於坐標面的平面去截三個曲面。所得截線方程為
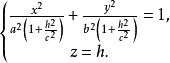雙曲面漸近錐面
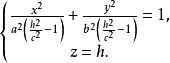雙曲面漸近錐面和
雙曲面漸近錐面它們都是橢圓，具有相同的中心和對稱軸，並且曲面對應的半軸分別為
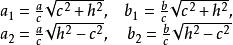雙曲面漸近錐面和
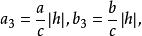雙曲面漸近錐面但它們的半軸的比相等
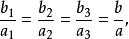雙曲面漸近錐面
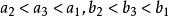雙曲面漸近錐面
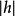雙曲面漸近錐面
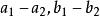雙曲面漸近錐面所以在平面z=h上截線橢圓的形狀相似，很明顯有。但當無限增大時，差趨於零。事實上
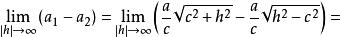雙曲面漸近錐面
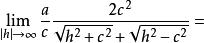雙曲面漸近錐面
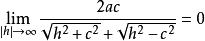雙曲面漸近錐面同理得
雙曲面漸近錐面 雙曲面漸近錐面可見，當無限增大時，三個曲面無限接近。即單葉雙曲面和雙葉雙曲面都與二次錐面(3)無限接近，我們稱二次錐面(3)是雙曲面(1)和(2)的漸近錐面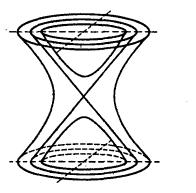(圖1) 。
圖1例題解析
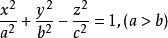雙曲面漸近錐面【例1】 用一族平行平面z=h(h為參數)截割單葉雙曲面得一族橢圓，求這些橢圓焦點的軌跡。
解：所截得的橢圓族方程為
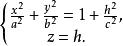雙曲面漸近錐面即
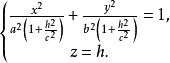雙曲面漸近錐面
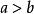雙曲面漸近錐面
雙曲面漸近錐面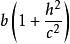
雙曲面漸近錐面因為，所以橢圓的長半軸為，短半軸為，從而橢圓焦點的坐標為
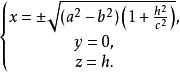雙曲面漸近錐面消去參數h得
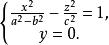雙曲面漸近錐面
雙曲面漸近錐面顯然這族橢圓焦點的軌跡是一條在坐標面上的雙曲線。雙曲線的實軸為x軸，虛軸為z軸 。
