定義
曲間的劃分(partition)
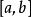 達布上和
達布上和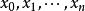 達布上和
達布上和定義:曲間 的一個劃分是指一個有限的序列 ,滿足
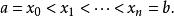 達布上和
達布上和達布和
 達布上和
達布上和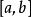 達布上和
達布上和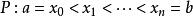 達布上和
達布上和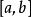 達布上和
達布上和定義1.設 是定義在曲間 上的函式,設 是 的一個劃分,設
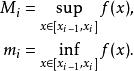 達布上和
達布上和記
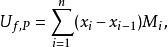 達布上和
達布上和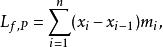 達布上和
達布上和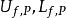 達布上和
達布上和稱 為關於劃分P的達布上和與達布下和 。
達布積分
 達布上和
達布上和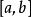 達布上和
達布上和定義2.設 是定義在曲間 上的函式,記
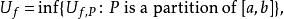 達布上和
達布上和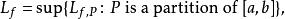 達布上和
達布上和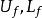 達布上和
達布上和 達布上和
達布上和稱 為 的達布上積分與達布下積分 ,或者,記為
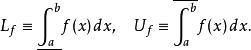 達布上和
達布上和達布可積
 達布上和
達布上和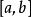 達布上和
達布上和 達布上和
達布上和定義3.設 是定義在曲間 上的函式,稱 是達布可積的,若
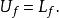 達布上和
達布上和性質
 達布上和
達布上和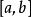 達布上和
達布上和以下總假定 是定義在曲間 上的函式。則達布和、達布積分各具有下列性質 :
1)對於任何給定的劃分,達布上總是大於或等於達布下和。且具有下列不等式成立:
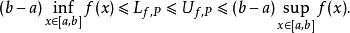 達布上和
達布上和2)達布積分滿足下列不等式:
 達布上和
達布上和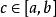 達布上和
達布上和3)對任意 ,
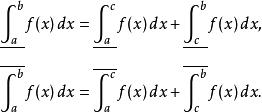 達布上和
達布上和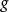 達布上和
達布上和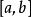 達布上和
達布上和4) 是定義在曲間 上的函式,
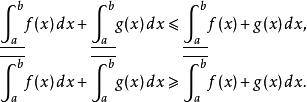 達布上和
達布上和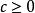 達布上和
達布上和5)對 ,
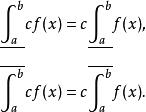 達布上和
達布上和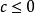 達布上和
達布上和6)對
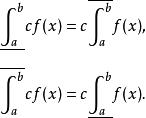 達布上和
達布上和7)
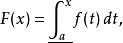 達布上和
達布上和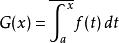 達布上和
達布上和是Lipschitz連續的。
例子
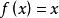 達布上和
達布上和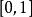 達布上和
達布上和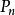 達布上和
達布上和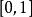 達布上和
達布上和 達布上和
達布上和設是定義在曲間上的函式,設劃分是將平均分割成等分。則有
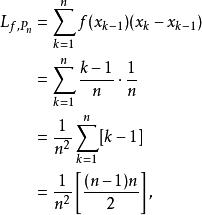 達布上和
達布上和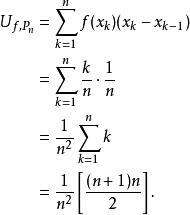 達布上和
達布上和因此,有
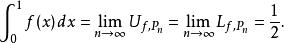 達布上和
達布上和