詳解
在卡魯扎-克萊因理論中,在降維之後,有效的普朗克質量隨著被壓縮的空間的體積的一些能量而變化。這就是為什麼在低維空間有效理論中體積變化可以產生 脹子 。
雖然弦理論自然地結合了卡魯扎-克萊因理論(首先引入了脹子),但是第一型弦理論,第二型弦理論和雜交弦理論等攝動弦理論在10維空間裡已經包含了最大數量的脹子。然而,另一方面,11維度的M-理論在其頻譜中不包括脹子,除非維度是緊緻化的。事實上,第二型弦理論中的脹子實際上是在一個圈上緊緻化的M-理論中的引力標量子,而E8 × E8弦理論中的脹子是Hořava-Witten模型的引力標量子。(關於脹子的M-理論起源的更多內容,見)。
在弦理論中,在世界面CFT(二維共形場理論)中也有一個脹子。其真空期望值的指數確定耦合常數g,為緊湊的世界面通過高斯-博內定理和歐拉示性數χ = 2 − 2g作為∫R = 2πχ,其中g是對手柄數進行計數的屬性,因此由特定世界面描述環或弦互動的數量。
 脹子
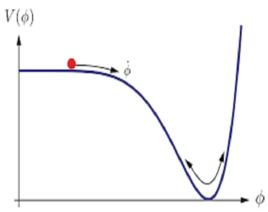
脹子因此,耦合常數是弦理論中的動力學變數,與量子場論中的常數不同。只要超對稱是不間斷的,這樣的標量場可以取任意值(它們是模數)。然而,超對稱破缺通常會為標量場產生一個勢能,並且標量場定位在一個最小值附近,在弦理論中其位置在原則上可以計算。
脹子類似於布蘭斯 - 迪克標量,有效的普朗克長度取決於弦的尺度和脹子場。
在超對稱中,脹子的超對稱粒子稱為脹微子(dilatino),脹子與軸子結合形成複雜的標量場。
脹子作用量
脹子重力的作用量是:
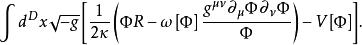 脹子
脹子這比真空中的布蘭斯 - 迪克理論更為普遍,因為有脹子勢能。