簡介
在數學中， 胡列維茨定理是代數拓撲的一個基本結論。定理通過“胡列維茨同態”將同倫論與同調論聯繫起來，是龐加萊此前部分結論的推廣。胡列維茨定理以維托爾德·胡列維茨命名。
定理陳述
胡列維茨定理是連線同倫群和同調群的關鍵一環。
絕對版本
對於任意空間X和任意正整數k，都存在群同態（構造見本小節末尾）
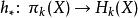胡列維茨定理稱為從k階同倫群到k階（整係數）同調群的胡列維茨同態。當k=1且X道路連通時，胡列維茨同態等價於標準的阿貝爾化映射
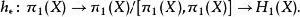胡列維茨定理
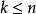胡列維茨定理
胡列維茨定理胡列維茨定理聲明，若X是(n-1)-連通空間，那么對於所有 ，胡列維茨同態都是群同構（當 ）或阿貝爾化（當n=1）。特別地，定理說明第一同倫群（即基本群）的阿貝爾化同構於第一同倫群：
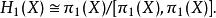胡列維茨定理
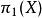胡列維茨定理因此，如果X道路連通且 是完美群，那么X的第一同調群為零。
胡列維茨定理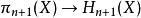
胡列維茨定理此外，當X是(n-1)-連通時（ ），胡列維茨同態 都是滿同態（滿射）。
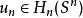胡列維茨定理
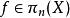胡列維茨定理
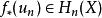胡列維茨定理胡列維茨同態由如下方式給定：設 為標準生成元，那么胡列維茨映射將同倫類 映射到 。
同調論
數學中， 同調論（homology theory）是拓撲空間“圈的同調”之直覺幾何想法的公理化研究。它可以寬泛地定義為研究拓撲空間的同調理論。
同倫
同倫（英語：homotopic，源自希臘語：ὁμός homós，意為“相同，相似的”與希臘語：τόπος tópos，意為“方位”）。在數學中，同倫的概念在拓撲上描述了兩個對象間的“連續變化”。 在拓撲學中，兩個定義在拓撲空間之間的連續函式，如果其中一個能“連續地形變”為另一個，則這兩個函式稱為 同倫的。這樣的形變稱為兩個函式之間的 同倫。同倫的一個重要的套用是同倫群和上同倫群的定義，它們是代數拓撲中重要的不變數。
事實上，在特定的空間中套用同倫還有一些技術上的困難。代數拓撲學家一般使用緊生成空間、CW復形或譜。
