相平衡關聯

相平衡關聯是將相平衡狀態下的溫度、壓力和各相組成等基礎數據，用經驗的或半經驗的方程進行關聯的方法。對於化工設計計算，特別是在套用電子計算機運算時，相平衡關聯式尤為適用。

相平衡關聯

正文

將相平衡狀態下的溫度、壓力和各相組成等基礎數據，用經驗的或半經驗的方程進行關聯的方法。基礎數據主要由實驗測定。將分散的實驗數據擬合成數學關聯式，就可以在實驗點之間內插或將實驗結果予以適當外推，甚至還能夠根據二元系(有時僅用純物質)的實驗數據來預測多元系的相平衡性質。對於化工設計計算，特別是在套用電子計算機運算時，相平衡關聯式尤為適用。
原理　根據相平衡準則，當 α相和β相達到相平衡時,任一組分i在 α相與β相中的逸度相等，即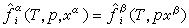。逸度弙姦和弙婑為溫度T、壓力p和組成(摩爾分數)x的函式，其間具體關係的確定,已超出經典熱力學範疇,必須依靠實驗測定，並套用統計力學或半經驗方法建立模型。這種模型包含一定數量的具有一定物理意義的模型參數θ1、θ2、……。將上述模型代入弙姦＝弙婑後,對於組分i,可寫出包含T、p、xα、xβ以及θ1、θ2、……的方程，即Fi(T,p,xα,xβ,θ1,θ2,…)=0。對於有k個組分的系統,可寫出有k個方程的方程組。將實驗得到的一系列T、p、xα、xβ數據代入上述方程組，就可回歸出模型參數。再通過弙姦＝弙婑，就可將T、p、xα、xβ聯繫起來，用於相平衡計算和有關化工過程的設計計算。
方法　化工上遇到的相平衡，大都是汽（氣）液或液液相之間的平衡。關聯這些相平衡的方法，有狀態方程法和活度係數法。
狀態方程法　利用狀態方程計算汽相或氣相和液相逸度的一種相平衡關聯方法。由熱力學導出的逸度弙i的計算式為：

式中R為摩爾氣體常數；V為混合物的體積；ni、nj為組分i 的摩爾數。如果已知混合物的狀態方程為p＝p(n1，n2，…，V，T，θ1，θ2，…)，代入式中，即可求得逸度。狀態方程在此用作聯繫弙i與 T、p、x的模型。相平衡至少涉及兩個相，因之選用狀態方程時，要求方程能兼用於系統所包含的兩個相。
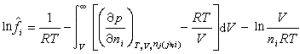
早就知道範德瓦耳斯方程能兼用於汽（氣）液兩相，但準確度不夠。最早用於準確計算汽液平衡的狀態方程是BWR方程，它是一個多參數方程,其關聯有足夠的準確度,然而外推常不夠理想。後來發展成為BWRS方程,可用於輕烴混合物以及含氮、二氧化碳和硫化氫的系統。經過改進的馬丁-侯方程，可取得與 BWRS方程類似的效果。近年來，更多注意比較簡單的三次型方程，如RK方程、SRK方程、PR方程等,它們對烴類系統也能取得較好的結果。
狀態方程法的最大優點是可以用統一的模型處理汽（氣）液兩相，避免了通常遇到的計算標準態逸度的困難，特別適用於高壓下較簡單系統的相平衡計算。對非理想性較強的系統(如含有強極性物質或有氫鍵的物質)，由於目前的狀態方程還不能有效地描述其汽（氣）液平衡，故這種系統須套用活度係數法。
活度係數法　利用活度係數方程來計算液相逸度的一種相平衡關聯方法。
對於汽（氣）相，逸度表達為：

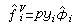
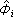式中yi為汽相中組分i的摩爾分數；為逸度係數。在低壓下,氣相常作為理想氣體混合物處理,這時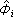=1。對於實際氣體，可由熱力學導出下述公式，利用狀態方程進行計算：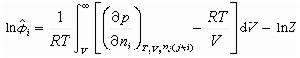

式中Z＝pV/nRT，為氣體混合物的壓縮因子。
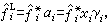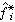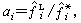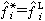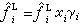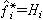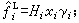對於液相，逸度弙忥表達式為：式中為標準態逸度；稱為活度, 它是對應於標準態的相對逸度,同時αi=xiγi,它等於摩爾分數xi與活度係數γi的乘積。標準態在原則上可以任意選取，在多數情況下取系統溫度和壓力下的液相純物質作為標準態。即(弙忥為液相純物質的逸度),於是;當γi＝1時,。此即路易斯-蘭德爾規則。符合此規則的混合物稱為理想溶液。當γi偏離1時,液相為非理想溶液，γi就是此溶液偏離理想程度的度量。有時在系統溫度下得不到液相純物質，例如臨界溫度低於系統溫度的氣體溶解於液體中，或固體組分溶解於液體中，對於這些氣體或固體組分,可取逸度等於亨利常數H的假想狀態作為標準態，即。於是，當γi=1時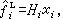，此即1803年英國W.亨利提出關於氣體溶解度的亨利定律。符合此定律的混合物，有時也稱為理想溶液，當然是遵守亨利定律意義上的理想溶液。極稀溶液中的溶質，通常符合亨利定律。
活度係數γi和過量自由焓GE之間，存在著如下的關係：

工程上常用的過量自由焓模型，以及由此導出的計算活度係數的方程（見表）均可按二元系寫出。

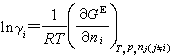
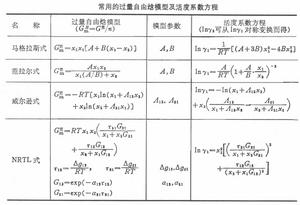相平衡關聯

過量自由焓是組分混合而成溶液時的自由焓變化與形成理想溶液時的自由焓變化之差。如果已知GE與T、p、x的關係，就可求得γi。與逸度相仿,確定GE與T、p、x的具體關係，也要建立模型──過量自由焓模型。將上述弙憓和弙忥的表達式代入相平衡準則得：

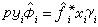
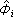式中由狀態方程求得；γi由過量自由焓模型求得，皆為溫度、壓力和組成的函式。此式將汽（氣）液平衡時溫度、壓力和汽（氣）液兩相組成聯繫起來。汽液相平衡比(Ki＝yi/xi)則相應地表述為：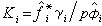

對於一般的非理想性不太強的二元系，這些方程都能達到較高的精度。對於非理想性很強的系統,如醇-烴二元系，只有威爾遜式和NRTL式適用。如果用於多元系，只需用二元參數即能預測多元系的相平衡。威爾遜式用得最廣泛，但它的缺點是不能用於液液平衡。NRTL式可用於液液平衡,但比威爾遜式多一個參數。此外,UNIUAC式有更嚴格的理論基礎，參數數目和威爾遜式相同，也可用於液液平衡，但形式較為複雜。威爾遜式、NRTL式和UNIQUAC式須用二元系實驗數據,回歸求得二元參數。但工程實際中，特別是新的化工過程開發時，常常缺乏實驗數據, 因而又發展出幾種基團貢獻法, 如SAOG法和UNIFAC法等，這些方法將實際系統看作是基團的混合物,任何組分都可由一些相對簡單的基團(如＝CH2、＝C＝O、-OH等）構成，從許多實驗數據回歸出這些基團對參數的貢獻，並列成表格，可以方便地用來計算任何未知的二元系和多元系的相平衡。
基團貢獻法準確度雖然稍差，但無需實驗數據，在工程上十分有用。活度係數法是目前工程上套用比較成熟的關聯方法。從發展來看，狀態方程法由於兩相使用統一的模型和不需標準態具有明顯的優點，正吸引著更多的注意。
套用　在化工設計中，不論是反應過程、傳質分離過程還是熱質傳遞過程，當涉及相際過程時，就需要進行T、p和各相組成間的相互推算，相平衡關聯主要為了解決這一課題。如一個二元汽液系統,已知液相組成x，要計算在一定壓力下的沸點和平衡汽相組成y;又如物流經過減壓閃急蒸餾或部分冷凝後，要計算汽液兩相的組成和數量，都須使用相平衡關聯所提供的溫度、壓力和各相組成的關係。

配圖

相關連線