面的置換表示
| 置換類型 | 置換的循環表示 | 不動圖像個數 |
| 不動 | (1) | 1 |
| 以面心-面心為軸轉±90度 | (1)(4) | 2x3=6 |
| 以面心-面心為軸轉180度 | (1)(2) | 3 |
| 以棱中-棱中為軸轉180度 | (2) | 6 |
| 以對角線為軸轉±120度 | (3) | 2x4=8 |
| 正六面體轉動群的階數為1+6+3+6+8=24 | ||
例：正6面體的6個面分別用紅、藍兩種顏色著色，有多少方案?
解：正六面體的面二著色問題，根據Polya定理，方案數為：
正六面體轉動群頂點置換表示
| 置換類型 | 置換的循環表示 | 不動圖像個數 |
| 不動 | (1) | 1 |
| 以面心-面心為軸轉±90度 | (4) | 2x3=6 |
| 以面心-面心為軸轉180度 | (2) | 3 |
| 以棱中-棱中為軸轉180度 | (2) | 6 |
| 以對角線為軸轉±120度 | (1)(3) | 2x4=8 |
| 正六面體轉動群的階數為1+6+3+6+8=24 | ||
例：用2種顏色給正6面體的8個頂點著色，有多少方案?
解：正六面體的頂點二著色問題，根據Polya定理，方案數為：
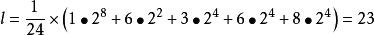正六面體轉動群棱的置換表示
| 置換類型 | 置換的循環表示 | 不動圖像個數 |
| 不動 | (1) | 1 |
| 以面心-面心為軸轉±90度 | (4) | 2x3=6 |
| 以面心-面心為軸轉180度 | (2) | 3 |
| 以棱中-棱中為軸轉180度 | (1)(2) | 6 |
| 以對角線為軸轉±120度 | (3) | 2x4=8 |
| 正六面體轉動群的階數為1+6+3+6+8=24 | ||
