模糊性數學
正文
研究和處理模糊性現象的數學理論和方法。1965年美國控制理論學者 L. A.扎德發表了論文《模糊集合》（或譯不分明集合、弗晰集合），標誌著這門新學科的誕生。現代數學建立在集合論的基礎上。集合論的重要意義，就某一側面看，在於它把數學的抽象能力延伸到人類認識過程的深處。一組對象確定一組屬性，人們可以通過指明屬性來說明概念（內涵），也可以通過指明對象來說明它。符合概念的那些對象的全體叫做這個概念的外延，外延實際上就是集合。從這個意義上說，集合可以表現概念，而集合論中的關係和運算又可以表現判斷和推理，一切現實的理論系統都有可能納入集合描述的數學框架。但是，數學的發展也是有階段性的。經典集合論只把自己的表現力限制在那些有明確外延的概念和事物上，它明確地限定：每一個集合都必須由確定的元素所構成，元素對集合的隸屬關係必須是明確的，絕不模稜兩可。對於那些外延不分明的概念和事物，經典集合論是暫時不去反映的，這屬於待發展的範疇。關於這一點，集合論發展的先驅之一(F.-É.-J.-) É.波萊爾就早有察覺，他曾借一個希臘悖論提出了這樣一個問題：究意有多少粒種子才夠得上是一堆？“一堆”這個概念的外延是什麼？它是由哪些自然數所構成？“……界限在哪裡？能不能說325647粒種子不叫一堆而325648粒就構成了一堆？”按照恩格斯的觀點：“辯證法不知道什麼絕對分明和固定不變的界限，不知道什麼無條件的普遍有效的'非此即彼'”，“一切差異都在中間階段融合，一切對立都經過中間環節而相互過渡。”禿與不禿是不能以某一頭髮根數來分界的,人與猿、脊椎動物與非脊椎動物、生物與非生物等等也都找不到確切的界線。從差異的一方到差異的另一方，中間經歷了一個從量變到質變的逐步過渡的過程,這種現象叫做差異的中介過渡性;處於中介過渡的事物顯示出亦此亦彼性質，由這種亦此亦彼性所引起的外延判斷和劃分上的不確定性就叫做模糊性。具有模糊性的事物和現象不能用經典集合論來刻畫。
模糊性現象是一種普遍存在的現象。以前人們迴避它，但是，由於現代科技所面對的系統日益複雜，模糊性總是伴隨著複雜性出現；各門學科，尤其是人文、社會學科及其他“軟科學”的數學化、定量化趨向把模糊性的數學處理問題推向中心地位；最重要的是，由於計算機科學的進展，要使計算機能像人腦那樣對複雜事物具有識別的能力，就必須研究和處理模糊性。從經典集合論向模糊集合擴展是歷史發展的要求。扎德的想法是很自然的。對論域U 中的子集A 可以通過它的特徵函式ⅹA來描述：
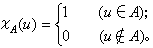
來近似表示,Aλ叫做A的λ截集。當λ從1下降至0，Aλ由小變大，{Aλ}說明了A可被看作是一個“可變的”、“有彈性”的、具有“游移邊界”的集合。扎德用隸屬度概念來表現處於中介過渡的事物對差異一方所持有的傾向性程度，從“亦此亦彼”中提取了“非此即彼”的信息。 用【0，1】中的一個實數來表示某一對象對某一概念的隸屬度,這是一種抽象。那么這種抽象究竟是否正確？隸屬度有客觀意義嗎?如何確定它?這是模糊性統計所研究的問題。波萊爾在解決“一堆”問題時，隱約顯露出這樣的構想：每次讓人報一個區間【ξ,+∞】以表示“一堆”的一個近似的外延，ξ是一個自然數，它隨人而異，隨時而異。統計這些區間對某一自然數n的覆蓋頻率,用它可以表示 n對於“一堆”概念的符合程度。現在有一種模糊統計模型正是按照這種思想建立的。大量試驗表明，類似於機率統計試驗中事件發生的頻率穩定性，在模糊性統計試驗中也存在著覆蓋頻率穩定性的規律，它說明了隸屬度概念是一種符合客觀實際的正確抽象。模糊性統計每次試驗所得到的是論域中的一個“集”，它是一種集值統計。隨機性反映因果律的破缺，它是由於條件不充分而導致的關於結果發生與否的不確定性；模糊性反映排中律的破缺，它是由於外延不分明而導致的對給定事物在是非判斷上的不確定性，二者是有區別的。但它們之間又有聯繫，這是正在深入研究的一個課題。
就像“價值“可以公度一切商品那樣，在一定條件下，隸屬度也可以公度一類模糊性的事物。諸如“效用度”、“滿意度“等這樣一些特殊的隸屬度，在管理決策理論中都扮演了統一量綱、化繁為一的重要角色。隸屬度具有可運算和變換的品格，這正是模糊集合論套用、發展的前提。扎德最初定義模糊集合運算如下：
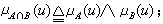
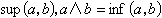,A∪B、A∩B分別叫A、B的並與交,Ac叫A的補集。當A、B蛻化成經典集合時,上述運算就是經典的集運算，所以上述模糊性集運算是經典集運算的進一步推廣。但是這種推廣不是惟一的，已有十幾種不同的模糊性集運算定義,研究各種運算的特性、適應條件、相互關係,這是“模糊運算元理論”所研究的內容。 隸屬度就是一個模糊性命題的真確程度，隸屬度運算聯繫著邏輯的真值演算。布爾邏輯的真值域是({0,1}，∨,∧)，它是一個布爾代數。扎德集運算所對應的是一種連續值邏輯,其真值域是(【0,1】,∨,∧)；它不再是一個布爾代數，因為它不再滿足互余律:α∨αc=1,α∧αc=0（對所有α∈【0,1】）,互余律反映了布爾邏輯的“非此即彼”性質。(【0,1】,∨,∧)叫做軟代數。軟代數有什麼代數性質?當以(【0,1】,∨,∧)取代({0,1},∨,∧)時,布爾邏輯會變成什麼樣子？更一般地，以(P(【0,1】),∨，∧)取代（這時得到模糊語言值邏輯）,又會得到什麼結果？這裡P(U)表示由U 的一切子集構成的集合,P(【0，1】)中的∨、 ∧按並、交運算定義。這些構成了“模糊邏輯代數”理論。格論是它特別重要的工具。
笛卡兒乘積U×V（見多重線性代數）的模糊子集R叫做從U 到V 的模糊關係。模糊關係在模糊集合的理論中占有比普通關係在普通集合論中更為重要的地位。設R、S分別是從U 到V、從V 到W 的模糊關係，定義合成關係R。S為：
。
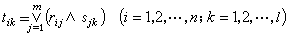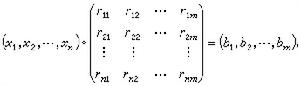
其中 
從純數學角度看，集合概念的擴充使許多數學分支都增添了新的內容。例如不分明拓撲、不分明線性空間、模糊測度與積分、模糊群、模糊範疇、模糊圖論，等等。其中有些領域，尤其是不分明拓撲，已有比較深刻的研究內容，為由來已久的格上拓撲學提供了新的背景與方法。
模糊性數學發展的主流是在它的套用方面。既然模糊性概念已經找到了模糊集的刻畫方式，那么人類運用概念進行判斷、評價、推理、規劃、決策和控制的過程也可以用模糊性數學的方法來逐步刻畫。例如，“模糊聚類分析”給出利用模糊關係來對事物進行模糊性劃分的方法；“模糊模型識別”給出了模糊性事物的識別方法；“模糊綜合評判”在多因素場合給出了對事物進行評定的方法；“模糊規劃”給出了模糊性限制條件下的規劃模型與解法；“模糊決策”給出了多目標情形下能反映決策者意志與經驗的決策方法；“模糊控制”給出了模糊性系統當精確數學模型難以建立而又有人的實際控制經驗可以採納時的控制方法。這些方法構成了一種模糊性系統理論，構成了一種思辨數學的雛形。它已經在醫學、氣象、結構力學、心理、經濟管理、計量、石油、地質、環境、生物、農業、林業、化工、紡織、語言、控制、遙感、雷達、教育、體育等等方面有了套用。在氣象、結構力學、控制、心理等方面已有具體的研究成果說明模糊性數學是該領域中的一項重要的數學工具。然而，模糊性數學最重要的套用領域是計算機智慧型。它已經被運用於專家系統和知識工程等方面。不少人認為它與新一代計算機的研製有緊密的聯繫。
模糊性數學還沒有成熟，對它也還存在著不同的意見和看法，有待實踐去檢驗。
參考書目
C.V.尼古塔、D.A.拉萊斯庫著,汪浩、沙鈺譯,《模糊集合在系統分析中的套用》,湖南科學技術出版社,長沙,1981。(C.V.Negoitǎ and D.A.Ralescu,Applications of Fuzzy Sets to Systems Analysis,Birkhuser, Basel, 1975.)
L.A.扎德著,陳國權譯,《模糊集合·語言變數及模糊邏輯》,科學出版社,北京,1982。(L.A.Zadeh The Concept of a Linguistic variable and Its Application toApproxiMate Reasoning,Elsevier,New York,1975.)
汪培莊編：《模糊集合論及其套用》，上海科學技術出版社，上海，1983。
