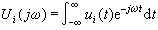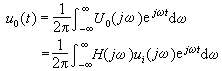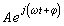暫態頻域分析
集總的線性時不變電路和系統的激勵與回響的關係都由常係數線性微分方程來描述。如果施加以正弦形激勵,如Asin(ωt+嫓),或指數形激勵,如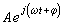 ,則其穩態回響一般亦呈同頻率的正弦或指數形式。採用複數相量法,只需求解由電路方程所得複數方程組,就可以求得所需的回響。
,則其穩態回響一般亦呈同頻率的正弦或指數形式。採用複數相量法,只需求解由電路方程所得複數方程組,就可以求得所需的回響。 暫態分析的目的是要研究在電路中施加激勵後所出現的回響。對於線性時不變電路和系統,暫態的頻域分析的基本思想是將激勵展開為許多存在於 -∞<t<∞的正弦形或複數指數函式形的諧波,再根據線性電路的線性性質分別計算各諧波在電路中產生的諧波回響。這一計算與穩態分析一樣,將所有的諧波的穩態回響相加即可得到所需的暫態回響。在激勵是周期性時間函式的情況下,將激勵展開為許多其頻率是激勵基波頻率K倍(K是整數)的諧波之和,即為激勵的傅立葉級數展開式,所得的回響亦表示為類似的級數形式。在激勵是非周期時間函式的情況下,激勵的展開式是頻率連續分布在-∞<ω<∞的多不可數的諧波之和,這便是激勵的傅立葉積分,所得的回響亦表示為類似的積分形式。
周期性時間信號的諧波分析 周期性連續時間信號是具有
g(t)=g(t+T0)T0≠0
性質的信號。滿足上式的最小的T0值稱為此信號的周期,其頻率為f0。滿足狄里赫利條件的周期性時間信號可以用傅立葉級數展開為一系列頻率為Kf0(K=整數)的簡諧時間函式之和
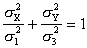 (1)
(1)
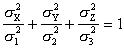
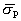
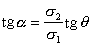
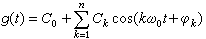 (2)
(2)
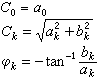
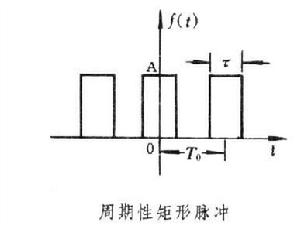 圖中的周期性矩形脈衝的傅立葉級數展開式是
圖中的周期性矩形脈衝的傅立葉級數展開式是 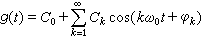
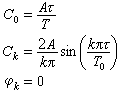
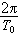 =Δω→dω,可以得到傅立葉積分變換式
=Δω→dω,可以得到傅立葉積分變換式 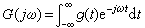 (3)
(3)
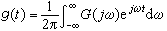 (4)
(4)
G(jω)=【g(t)】 (5)
g(t)=-1【G(jω)】 (6)
對式(4)可以作這樣的解釋:g(t)中頻率為ω的簡諧分量的復振幅以密度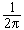 G(jω)分布在ω軸上,將這些頻率連續分布在(-∞,∞)上的所有諧波相加(積分)即得到g(t)。G(jω)是複數,它的模和幅角都是頻率ω的函式。將G(jω)記作
G(jω)分布在ω軸上,將這些頻率連續分布在(-∞,∞)上的所有諧波相加(積分)即得到g(t)。G(jω)是複數,它的模和幅角都是頻率ω的函式。將G(jω)記作 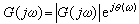 (7)
(7)
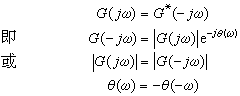 即幅頻函式是ω的偶函式,相頻函式是ω的奇函式。
即幅頻函式是ω的偶函式,相頻函式是ω的奇函式。 套用 集總的線性系統的輸入激勵與輸出回響的關係可以用一常係數線性微分方程表示
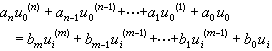 (8)
(8)
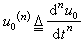 等。對於形如ejwt的激勵,式(8)所表示的系統的傳遞函式為
等。對於形如ejwt的激勵,式(8)所表示的系統的傳遞函式為 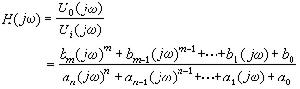 對於任一形式的激勵 ui(t)作用於此系統所產生的回響u0(t),便可通過將ui作傅立葉變換,得其頻譜密度
對於任一形式的激勵 ui(t)作用於此系統所產生的回響u0(t),便可通過將ui作傅立葉變換,得其頻譜密度