基本介紹
同類基本形間的射影對應叫做同素射影對應，同素射影對應是一種特殊的射影對應，例如，把點變成點，或直線變成直線的射影對應都稱為同素射影對應。
相關介紹
射影對應是射影幾何中最重要的一種對應，通常指射影空間(平面、直線)之間保持共線性和共線四點的交比不變的點的一一對應。在兩個射影空間(平面、直線)都建立了射影坐標系後，它們之間的射影對應可以用對應點坐標之間的關係表出。例如，對於兩個射影平面π與π′，若平面π上點P的射影坐標為x，x，x，其對應的π′上點P′的射影坐標為x′，x′，x′，則射影對應有代數表達式
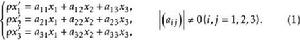同素射影對應其中ρ≠0是齊次坐標的比例常數，|(a)|是矩陣(a)的行列式。因此，也可以直接用點的射影坐標之間的齊次非奇異線性變換(1)來定義射影對應。當兩個對應的射影空間(平面、直線)重合時，這種集合到自身的射影對應，通常稱為射影空間(平面、直線)的射影變換.在射影空間(平面、直線)中建立射影坐標系後，射影變換可以用對應點的坐標之間的關係表出。例如，在射影平面上把具有射影坐標x，x，x的點變成具有射影坐標x′，x′，x′的點的射影變換同樣有代數表達式(1)。因此，同樣可以直接用點的坐標的齊次非奇異線性變換(1)來定義射影變換 。
二維變換指點場到點場，線場到線場的變換，點場和線場是二維基本形，平面上所有點的集合叫點場，平面上所有直線的集合叫線場。
非奇線性對應必是平面π上與平面π'上點之間的一一對應，平面π上的點到平面π'上的點的非奇性對應建立了π上的直線到π'上的直線的非奇線性對應。也就是點場到點場的非奇線性對應必建立線場到線場的非奇線性對應。射影對應也可以定義為滿足共線點的象仍是共線點，且任何共線四點的交比等於對應四點的交比的一一對應。同樣可以定義線場到線場之間的射影對應定義。
兩平面的點之間的透視對應必是射影對應；點場到點場或線場到線場的射影對應叫同素射影對應，因點場與線場是對偶圖形，四對對應元素(如四對對應點，每三點不共線)可確定非奇線性對應，即有四個獨立條件，再給定一點P，則可唯一確定其對應點P'，若P(i=1,2,3,4)四點中無三者共線,那么使這四點不變的射影變換一定是恆等變換，即非恆等的射影變換不能有四個不變點 。
