線性常微分方程
正文
微分方程中出現的未知函式和該函式各階導數都是一次的,稱為線性常微分方程。它的理論是常微分方程理論中基本上完整、在實際問題中套用很廣的一部份。線性一階常微分方程 在初等常微分方程中已經知道方程
y┡+p(x)y=Q(x) (1)
及其對應的齊次線性方程y┡+p(x)y=0 (2)
的解法,得到(2)的通解和滿足初始條件y(x0)=y0的特解分別為: (3)
(3)
 , (4)
, (4)

①y(x)呏0是(2)的解,稱為明顯解。如果p(x)在x0連續,則滿足零初始條件y(x0)=0的解必為明顯解。②方程(2)的任意兩個解y1與y2的線性組合 C1y1+C2y2也是(2)的解,C1,C2是任意常數。③y*(x)是(2)的滿足條件y(x0)=1的特解。④(2)的解的全體構成一維線性空間,明顯解是零元素。⑤ 方程(1)的通解(4)等於(1)的一個特解加上(2)的通解。⑥ Y(x )是(1)的滿足零初始條件y(x0)的特解。⑦若Q(x)=Q1(x)+Q2(x),又已知yi(x)是y┡+p(x)y=Qj(x),(i=1,2)的解,則y1(x)+y2(x)是方程(1)的解(疊加原理)。
易見,線性代數方程組的解也具有類似的性質。線性常微分方程組和線性高階常微分方程的解也有同樣的性質。
線性一階常微分方程組 這種方程組可寫成如下形式
 (6)
(6)

為方便計,(6)可寫為向量方程
 (7)
(7)

 (8)
(8)
 (9)其中
(9)其中 
對應於方程(1)與(2)的前述7條性質,方程(7)與(8)也有如下的性質。①y(x)呏0是(8)的明顯解。若A(x)在x0連續,則滿足條件y(x0)=0的解必為明顯解。②方程(8)的任意幾個解的線性組合也是(8)的解。(8)的通解可表為
 ,其中C1,C2,…,Cn為n個任意常數,y1(x),y2(x),…,yn(x)是(8)的任何n個線性獨立解,稱之為(8)的一個基本解組,由它們的n2個分量構成的方陣稱為基解方陣。③若y壜(x),(i=1,2,…,n)是(8)的基本解組,使對應的基解方陣Y*(x)滿足初值條件Y*(x0)=E(E為單位方陣),則(8)的任一解y(x)可表示為y(x)=Y*(x)y(x0)。但僅當
,其中C1,C2,…,Cn為n個任意常數,y1(x),y2(x),…,yn(x)是(8)的任何n個線性獨立解,稱之為(8)的一個基本解組,由它們的n2個分量構成的方陣稱為基解方陣。③若y壜(x),(i=1,2,…,n)是(8)的基本解組,使對應的基解方陣Y*(x)滿足初值條件Y*(x0)=E(E為單位方陣),則(8)的任一解y(x)可表示為y(x)=Y*(x)y(x0)。但僅當 與A(t)為可交換時(即B(t)A(t)=A(t)B(t)),Y*(x)才能寫成
與A(t)為可交換時(即B(t)A(t)=A(t)B(t)),Y*(x)才能寫成 的形式。④(8)的解的全體構成n維線性空間,任何一個基本解組都可作為此空間的基底,明顯解是零元素。⑤方程(7)的通解等於它的一個特解加上(8)的通解,且可表示為:
的形式。④(8)的解的全體構成n維線性空間,任何一個基本解組都可作為此空間的基底,明顯解是零元素。⑤方程(7)的通解等於它的一個特解加上(8)的通解,且可表示為:  (10)
(10)
 的解,則y1(x)+y2(x)是(7)的解。
的解,則y1(x)+y2(x)是(7)的解。 線性高階常微分方程 這種方程可寫為如下形式
 。 (11)
。 (11)


 ,而朗斯基行列式成為
,而朗斯基行列式成為 
由於黎卡提方程 y┡=p(x)y 2+Q(x)y+R(x)可借代換
 化為u的線性二階方程
化為u的線性二階方程 
 。
。
y"+p1(x)y┡+p2(x)y=0 (13)
的一個非零特解y1為已知,則可求出它的通解,且具有如下形式: ,
,
y"+p1(x)y┡+p2(x)y=q(x), (14)
僅當已知它的兩個特解時才能求出其通解;對於n=2時的方程組(7),也是如此。方程(13)在套用數學中頗為重要,對它還有冪級數解法、廣義冪級數解法、定積分解法以及解的定性討論等內容。
伴隨微分方程 以A*(x)記方程(8)中A(x)(可能為複方陣函式)的共軛轉置方陣,則稱
 (15)
(15)
Ψ*(x)φ(x)=C,
C是(復的)常數方陣。藉助於(12),易證線性齊次高階方程
Lny=y(n)+p1(x)y(n-1)+…+pny=0 (16)
的伴隨方程是
 , (18)
, (18)
 。
。
 (19)
(19)
常係數線性方程組與常係數線性高階方程 對於常係數一階線性非齊次方程組
 (20)
(20)
 。 (21)
。 (21)
 。 (22)
。 (22)
 。 (23)
。 (23)
稱λ的n次代數方程│A-λE│=0為(21)的特徵方程,它的根為(21)的特徵根。可以證明:若λi是特徵根,Γi是對應的特徵向量,則e
 Γi是(21)的解;又若λi≠λj都是特徵根,則e
Γi是(21)的解;又若λi≠λj都是特徵根,則e Γi與e
Γi與e Γj是(21)的兩個線性獨立解。因此,如果(21)有n個不同的特徵根λ1,λ2,…,λn,則它的通解是
Γj是(21)的兩個線性獨立解。因此,如果(21)有n個不同的特徵根λ1,λ2,…,λn,則它的通解是  。
。
 , (24)
, (24)


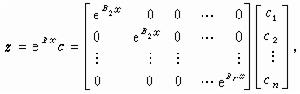
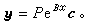 (25)
(25)
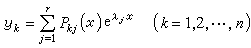 (26)
(26)
若(20)與(21)是由線性常係數高階方程
y(n)+p1y(n-1)+…+pny=q(x) (27)
與y(n)+p1y(n-1)+…+pny=0 (28)
化來,則特徵方程是λn+p1λ(n-1)+…+pn-1λ+pn=0, (29)
而(26)中的y1即(28)的通解。這時A的右上角有一個n-1階子行列式之值為1,故(29)的每一i重根λ*只對應於一個i階若爾當塊,而y1中 前面的多項式必為i-1次。又若(27)為實係數而有復特徵根,則必成對出現。實用上常以 eαxcosβx與eαxsinβx這兩實解代替兩個共軛復解
前面的多項式必為i-1次。又若(27)為實係數而有復特徵根,則必成對出現。實用上常以 eαxcosβx與eαxsinβx這兩實解代替兩個共軛復解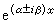 。
。 雖然從理論上說,(20)或(27)的特解可按公式(23)右邊的第二項來求,其中eAtt=peBttp-1。但在具體計算時是相當麻煩的。當q(x)或ƒ(x)的各分量為多項式、正弦餘弦函式、指數函式、或三者的乘積之和時,不難得知對應的特解所應具有的形式,然後可用待定係數法來求特解。此外,也可採用符號方法或拉普拉斯變換法求特解。拉氏變換法是把常係數線性微分方程的求解問題化為線性代數方程或方程組的求解問題,求解時把初始條件一起考慮在內,不必先求通解再求特解,在工程技術中有廣泛的套用。此外,還有用留數理論求方程(20)或(21)解的方法。
歐拉方程和周期係數線性方程 這是兩種可化為常係數的變係數線性方程。二者有本質的不同,前者是切實可行的,後者只有理論上的價值。歐拉方程是形如
xny(n)+α1x(n-1)y(n-1)+…+αn-1xy┡+αny=ƒ(x)(30)
的方程,經自變數的代換x=et就可化為常係數,這時有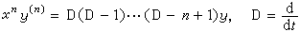 ,
,
(αx+β)ny(n)+α1(αx+β)(n-1)y(n-1)+…+αny=ƒ(x)可作代換αx+β=et。又對方程組(7),只要αij(x)=αijφ(x)對一切i,j,則用代換 總可把(7)化為常係數。
總可把(7)化為常係數。
若(8)中的A(x)對x有周期ω,而Y(x)是一基解方陣,則Y(x+ω)也是,故Y(x+ω)= Y(x)C,C為非奇異方陣。由線性代數知有方陣B使C=eωB,令p(x)=Y(x)e-Bx,則p(x)也有周期ω。若在(8)中作變換y=p(x)z,則z將滿足常係數方程
 。 (31)
。 (31)
 ,ρi與λi分別稱為周期係數方程(8)的特徵乘數和特徵指數。由(31)易見這時(8)的任意解的每一分量是形如e
,ρi與λi分別稱為周期係數方程(8)的特徵乘數和特徵指數。由(31)易見這時(8)的任意解的每一分量是形如e ·φi(x)的函式的線性組合,其中φi(x)為x的多項式,係數是x的周期為ω的周期函式。但即使對於極簡單的馬蒂厄方程
·φi(x)的函式的線性組合,其中φi(x)為x的多項式,係數是x的周期為ω的周期函式。但即使對於極簡單的馬蒂厄方程 y"+(λ+μcosx)y=0, (32)
對應的一階方程組的變換方陣 C也寫不出來,而只知有ρ1ρ2=1這個關係式。為研究 (32)的解的性質,只能在(λ,μ)平面中畫出無數條曲線(它們的方程只能近似地確定),分此平面為無數個屬於兩種類型的區域,然後說明在兩類區域中或位於曲線上的點(λ,μ),其所對應的方程(32)的解會具有一些什麼樣的性質。關於方程(32)以及比它更廣的很有實用價值的希爾方程y"+φ(x)y=0,φ(x+π)=φ(x)
都有專著。參考書目
葉彥謙編:《常微分方程講義》,第2版,人民教育出版社,北京,1982。
R.貝爾曼著,張燮譯:《常微分方程的解的穩定性理論》,科學出版社,北京,1957。(R.Bellman,StαbilityTheory of Differentiαl Equαtions, McGraw-Hill,New York, 1953.)
E.L.Ince,Ordinαry Differentiαl Equαtions, Dover, New York, 1944.

