正文
單元是元件、器件、部件、設備等的泛稱。單元或系統的功能喪失，無論其能否修復，都稱之為失效。可靠性理論即以失效現象為其研究對象，因而涉及工程設計、失效機理的物理和化學分析、失效數據的收集和處理、可靠性的定量評定以及使用、維修和管理等範圍。可靠性問題的提出，是由於大工業生產及第二次世界大戰中研製和使用複雜的軍事裝備的需要。雖然單元的可靠性不斷有很大的提高，但是由於大型系統的結構越來越複雜，要求其完成的功能也越來越廣泛，因此定量評定和改善系統可靠性已成為一個重要課題。
通過數學模型定量研究系統的可靠性，並探討它與系統性能、經濟效益之間的關係，是可靠性數學理論的主要方法之一。
可靠性的數量指標 假定系統只有正常和失效兩種狀態。系統在失效前的一段正常工作時間稱為壽命。由於失效是隨機現象，因此，壽命可用非負隨機變數X 及其分布函式F(t)=P{X ≤t}（見機率分布）來描述。
對失效後不加修復的單元，其可靠性用可靠度來刻畫。單元在時刻t的可靠度R(t)定義為:在一定的工作條件下在規定的時間【0，t】中完成其預定功能的機率。因此,若單元的壽命為X，相應的壽命（或失效）分布函式為F(t)，則R(t)=P{x>t}=1-F(t),其中t≥0。根據上式的機率含義，可靠度R(t)又稱為生存函式。
一個生存到時刻t的單元，稱之為有年齡t。在其後長度為x的區間中失效的條件機率為
存在,則r(t)稱為時刻t的(條件)失效率。當Δt很小時,r(t)Δt可解釋為單元生存到t時刻的條件下,在(t,t+Δt】中失效的機率。當X是連續型隨機變數，即F′(t)=ƒ(t)存在時,則有r(t)=ƒ(t)/R(t)，R(t)>0,此時r(t)與R(t)之間有如下的基本關係R(t)＝
。因此，F(t)、R(t)或r(t中任意一個都可用來描述不可修復單元的壽命特徵。 對失效後可修復的系統，其狀態隨時間的進程是正常與失效相交替的一個隨機過程。它的可靠性由不同的指標來描述:系統首次失效前的時間T的機率分布及均值；任一時刻t系統正常的機率，即可用度；(0,t】中系統失效次數的分布和均值等。
壽命數據統計分析、壽命分布及分布類、結構函式、網路可靠性、故障樹分析、複雜系統可靠性分析以及可靠性中的最最佳化等，是可靠性數學理論的主要研究內容。
壽命數據統計分析 壽命數據的收集和分析是可靠性定量評定的基礎。主要討論壽命分布類型的確定及其參數估計。由於壽命試驗費錢、費時，試驗常常不能等到所有受試樣本都失效時才結束，此外，現場數據中可能有中途失去觀察的情形，因此獲得的壽命數據往往是不完全的樣本。對於這類不完全樣本的參數估計和分布類型檢驗，在數理統計中有專門的方法來處理，其中以壽命分布是指數時，結果最簡單(見壽命數據統計分析)。
壽命分布及分布類 在實際中以下的壽命分布最常使用：
① 指數分布
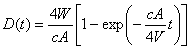，式中t≥0，而λ>0為參數。指數分布的失效率是常數λ,適用於描述某些電子元器件使用期的壽命。 ② 韋布爾分布
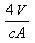稱為尺度參數，λ稱為形狀參數，λ=1即為指數分布。韋布爾分布的失效率為 
，
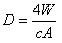，當 λ<1時，r(t)是單調遞減的；當λ>1時，r(t)是單調遞增的；當λ＝1時，r(t)＝λ。由於韋布爾分布的參數適應範圍大，已廣泛用於描述金屬疲勞、真空管、軸承等的壽命。 研究壽命分布的共同性質，需要引入壽命分布類的概念。若對任意固定的x≥0,F(x|t)是t≥0的遞增函式，即在同樣長的時間間隔x中，單元失效的機率隨年齡t增加，則F稱為屬於失效率遞增類,記為F∈IFR。當r(t)存在時，F∈IFR等價於r(t)遞增。相仿地，可定義失效率遞減類，以及失效率平均遞增或遞減的類等。
壽命分布類研究中的典型問題有：由屬於同一分布類的單元所組成的系統，其壽命是否屬於相同的類，以及考察其可靠度界等。
結構函式 反映單元的狀態及由這些單元組成的系統的狀態之間的關係。假定系統由n個單元組成,單元與系統都只有兩個狀態:正常和失效,分別用1和0表示。用變數xi(取值0或1)表示單元i的狀態,尣=(x1,x2,…,xn)是單元的狀態向量，用函式φ(尣)表示系統的狀態，其定義為：
通常的系統具有如下的性質：任一單元的失效不會使系統性能改善；系統中不包含多餘的對其性能不發生影響的單元。這種系統稱為關聯繫統。這一性質可用結構函式來表達：設φ(尣)是系統的結構函式。對任意的狀態向量尣≤у，有φ(尣)≤φ(у),其中尣≤у表示各xi≤yi；對任意的i（1≤i≤n）,存在狀態向量尣使φ（0i,尣）=0，φ(1i, 尣)=1,其中(0i,尣)及(1i,尣)表示尣的第i個分量分別以0和1代替後所得的向量。
典型的關聯繫統有：串聯繫統，即其中任一單元失效則系統失效；並聯繫統，即當所有單元失效時，則系統失效；k-out-of-n(F)系統,即當其中k或k個以上的單元失效時系統就失效，它是串聯或並聯繫統的推廣。在實際中,常用的2-out-of-3(F)系統是由三個單元組成而按多數單元的狀態進行表決的系統。這三種系統的結構函式分別為
網路可靠性 許多實際系統都可抽象成網路。例如計算機網際網路、通訊網路、輸油輸氣網路等。假定一個網路的頂點和邊（見圖論）只有正常和失效兩種狀態，而失效是互相獨立的，且已知每個頂點和邊正常的機率。從某一頂點能把信息傳送到另一個（或 k個）指定的頂點的機率，稱為網路的可靠度。在網路可靠度的計算中，因其結構複雜而必須尋找簡化網路的方法以及有效的算法，並比較不同算法的優劣。近年來已出現了不少較好的算法，關於計算的複雜性問題也有進展。
故障樹分析 簡稱 FTA。用演繹法按事件發生的前後邏輯關係，找出引起系統失效或某個不希望出現的事件（稱作頂端事件）發生的所有事件的可能組合。例如，研究鍋爐爆炸事件T。造成爆炸的原因有諸如壓力過大等種種事件A,B,…,D。若A，B，…，D之一發生就會引起T發生，則T與這些事件之間的關係就由邏輯門“或”來表示；若A、B同時發生才引起T發生,則T與A、B之間的關係就由邏輯門“與”來表示;循此下去,對A，B，…，D諸事件逐一分析,直到找出最基本的失效原因（基本事件）為止。這一過程可表示如圖
，其形狀如倒植的樹，所以稱之為故障樹,其中
表示“或”門;
表示“與”門;
表示事件；○表示基本事件。 對一個頂端事件T 進行故障樹分析時，其基本步驟是:建立故障樹；定性評定,即找出引起T發生的所有可能的基本事件的組合；定量評定，即根據基本事件發生的機率求T發生的機率。
FTA起源於20世紀60年代初,已用於宇宙航行、核電站安全分析等產業部門。由於這種方法形象直觀，便於工程和管理人員使用。這一方法的弱點是建立故障樹頗費時間和人力，對於複雜的系統，還難免會漏掉一些重要的失效原因。此外，評定複雜的故障樹必須藉助於計算機來進行。
對於包含有“非”門及其他邏輯門的故障樹的評定方法以及利用計算機輔助建立故障樹等,都是目前FTA研究的中心。
複雜系統可靠性分析 一個由1000個單元組成的系統是常見的，若每個單元的可靠度為0.999,單元間彼此獨立，任一單元失效均使系統失效，則系統的可靠度為
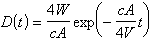可見相當之低。因此為提高系統的可靠度（可用度）,可採用備件並聯工作等手段,或者在系統中引入修理和更換。討論的問題有：已知系統的結構、單元的壽命和修復（或更換）時間分布、系統中修理工數目和修理規則等，研究系統可靠性的定量指標或者探討如何合理確定修理工數目或修理規則，使某個目標函式達到最優。通過數學模型，使用馬爾可夫過程、更新過程、馬爾科夫更新過程、補充變數法等分析方法進行研究，其處理手法與排隊論相近。 例如，由一個單元構成的最簡單的系統。若系統的壽命和修復時間有參數λ、μ的指數分布,且互相獨立。設時刻t=0時系統正常,且失效後修復的系統與新的一樣。則系統首次失效前的時間有參數λ的指數分布。利用馬爾科夫過程或更新過程可得到時刻t的可用度
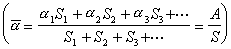
這表示在穩態下就平均而言，系統可資利用的時間所占的比例，等於一個周斯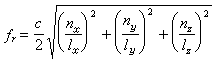
中正常工作時間
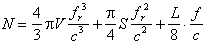所占的比例。這個公式為工程技術界廣泛採用。 當系統結構複雜時，一般求不出可靠性指標的解析式，常用計算機模擬。
可靠性中的最最佳化 包括更換策略以及備件最最佳化問題。
在許多場合，一個運行中的單元失效所帶來的損失，遠比更換一個未失效單元的費用大得多，因此把那些年齡長的單元及時更換下來是具有實際意義的。從而，要研究不同更換策略下系統可靠性指標的改善以及選擇最優策略的問題。
典型的策略有：按年齡更換策略，即當單元年齡到T時或單元在T前失效時進行更換。成批更換策略，即系統在失效時或在時刻kT(k=1,2,…)進行更換。
假定每次更換的費用對失效單元為с1，對未失效單元為с2(с2<с1),則在【0,t】中平均費用為
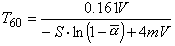
，這裡N 1(t)、N 2(t)分別為【0,t】中失效數和未失效而更換的單元數,E為數學期望。對有限時間t,或無限時間，目標函式分別選作【0,t】中平均費用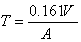
或極限平均費用
。所謂策略最最佳化問題，是指確定最佳更換時間T使目標函式值最小。 備件最最佳化問題,是研究在一定的資源(如費用、重量、體積等)限制下,如何合理地確定備件數目使系統可靠度達極大。
典型的問題是系統由k個獨立的級串聯而成，第j級由nj個獨立同型的單元並聯組成，每個單元的可靠度為pj。假定第j 級要用第i種資源，用量為gij(nj), 它是nj的嚴格增函式。資源i 的總量為bi，i=1，2,…,m，j=1，2，…,k。求最佳單元配置數目n=(n1,n2,…,nk)，使系統可靠度
在約束條件 
參考書目
曹晉華、程侃著：《可靠性數學引論》，科學出版社，北京，1986。
R.E.Barlow and F.Proschan,Statistical Theoryof Reliability and Life Testing, Holt, Rinehart and Winston, New York, 1975.
