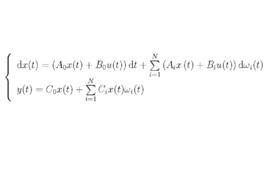基本概念
隨機控制系統是受隨機因素影響的動態系統。線性系統是指同時滿足疊加性與均勻性(又稱為其次性)的系統。
線性隨機系統即同時滿足線性系統和隨機控制系統特性的系統,它滿足線性系統的疊加性與均勻性,同時又受隨機因素影響。線性隨機系統分為連續線性隨機系統和離散線性隨機系統 。
連續時間線性隨機系統
考慮如下形式的連續時間隨機線性系統:
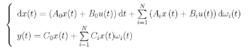 線性隨機系統
線性隨機系統其中
 線性隨機系統
線性隨機系統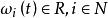 線性隨機系統
線性隨機系統分別表示系統的狀態,控制和輸出向量。 為定義在全機率空間
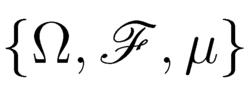 線性隨機系統
線性隨機系統上的隨機變數序列,且為獨立的廣義穩定的二階矩過程。對於給定的初始條件x (0) = x0 ,我們定義其相應的解過程為x (t, x0),輸出過程為y (t, x0)。定義矩陣組A,B,C如下:
 線性隨機系統
線性隨機系統均方穩定性
對於上述連續時間隨機線性系統,當u (t)=0,t>=0時,如果有
 線性隨機系統
線性隨機系統成立,就稱該系統為均方穩定的,簡稱矩陣組A是均方穩定的。
均方鎮定性
對於上述連續時間隨機線性系統,若存在矩陣K,使得當u(t) =Kx(t)時,下述閉環系統
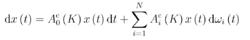 線性隨機系統
線性隨機系統對任意的初始條件x0 2 Rn為均方穩定的,那么就稱系統(2-13)為可鎮定的。簡稱(A,B)為均方可鎮定的。
其中,
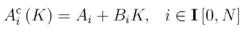 線性隨機系統
線性隨機系統能檢測性
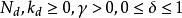 線性隨機系統
線性隨機系統如果存在常數使得
 線性隨機系統
線性隨機系統那么就稱(A,C)為能檢測的。
其中
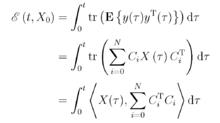 線性隨機系統
線性隨機系統該函式可以看成是連續時間線性隨機系統的輸出能量函式。
能觀測性
 線性隨機系統
線性隨機系統如果存在常數使得
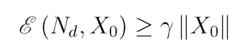 線性隨機系統
線性隨機系統對任意初始條件x0成立,則稱連續時間線性隨機系統為能觀測的。
離散時間線性隨機系統
我們考慮如下形式的離散時間隨機線性系統:
 線性隨機系統
線性隨機系統能檢測性
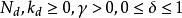 線性隨機系統
線性隨機系統如果存在整數> 0使得
 線性隨機系統
線性隨機系統那么我們說(A,C)是能檢測的。
能觀測性
 線性隨機系統
線性隨機系統對於離散時間隨機系統,如果存在常數使得
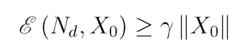 線性隨機系統
線性隨機系統成立,則稱連續時間線性隨機系統為能觀測的。