正合形式

正合形式是可表示為另一微分形式的外微分的微分形式，每個正合形式必定是閉形式。

簡介

正合形式是可表示為另一微分形式的外微分的微分形式。

設M是微分流形，α是M上的一個p形式。若存在(p-1)形式β，使得α=dβ，則稱α為正合p形式，簡稱正合形式。

由於外微分d有性質d=0，故每個正合形式必定是閉形式。

外微分

一個k階的微分形式的外微分是一個k+1階的微分形式。

對於一個k-形式ω =fdx在 R上，其定義如下：

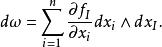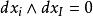正合形式

正合形式

對於一般的k-形式 Σfdx（其中多重指標I取遍所有{1, ...,n}的基數為k的有序子集），只作了線性推廣。注意如果上面有i=I則 。

閉形式

閉形式是一類外微分形式。

外微分為零的外微分形式，即，滿足dω=0的外微分形式ω稱為閉形式。

因為d=0，所以任何微分形式θ的外微分dθ是閉形式。