起源
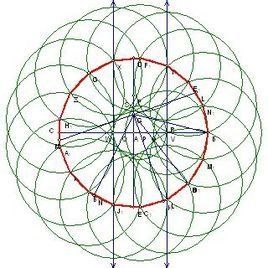 正十七邊形
正十七邊形最早的十七邊形畫法創造人是高斯【1801年數學家高斯證明:如果費馬數k為質數,那么就可以用直尺和圓規將圓周k等分.但是,高斯本人實際上並不會做正十七邊形。第一個真正的正十七邊形尺規作圖法直到1825年才由約翰尼斯·厄欽格(Johannes Erchinger)給出.】
。高斯(1777─1855年)德國數學家、物理學家和天文學家。高斯在童年時代就表現出非凡的數學天才。年僅三歲,就學會了算術,八歲因運用等差數列求和公式而深得老師和同學的欽佩。大學二年級時得出正十七邊形的尺規作圖法,並給出了可用尺規作圖的正多邊形的條件。解決了兩千年來懸而未決的難題,1799年以代數基本定理的四個漂亮證明獲博士學位。高斯的數學成就遍及各個領域,在數學許多方面的貢獻都有著劃時代的意義。並在天文學,大地測量學和磁學的研究中都有傑出的貢獻。
作法
先計算或作出cos(360°/17)
設正17邊形中心角為a,則17a=360°,即16a=360°-a
故sin16a=-sina,而
sin16a=2sin8acos8a=4sin4acos4acos8a=16sinacosacos2acos4acos8a
因sina不等於0,兩邊除之有:
16cosacos2acos4acos8a=-1
又由2cosacos2a=cosa+cos3a(三角函式積化和差公式)等
注意到cos15a=cos2a,cos12a=cos5a(誘導公式)等,有
2(cosa+cos2a+…+cos8a)=-1
令
x=cosa+cos2a+cos4a+cos8a
y=cos3a+cos5a+cos6a+cos7a
有:
x+y=-1/2
又xy=(cosa+cos2a+cos4a+cos8a)(cos3a+cos5a+cos6a+cos7a)
=1/2(cos2a+cos4a+cos4a+cos6a+…+cos14a+cos15a)
經計算知xy=-1
因而:x=(-1+√17)/4,y=(-1-√17)/4
其次再設:x1=cosa+cos4a,x2=cos2a+cos8a
y1=cos3a+cos5a,y2=cos6a+cos7a
故有x1+x2=(-1+√17)/4
y1+y2=(-1-√17)/4
最後,由cosa+cos4a=x1,cosacos4a=(y1)/2
可求cosa之表達式,
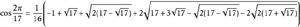 正十七邊形
正十七邊形它是有理數的加減乘除平方根的組合, 故正17邊形可用尺規作出
做法
 正十七邊形
正十七邊形給一圓O,作兩垂直的直徑AB、CD.
在OB上作E點使OE=1/4AO,連結CE.
作∠CEB的平分線EF.
作∠FEB的平分線EG,交CO於P.
作∠GEH=45°,交CD於Q.
以CQ為直徑作圓,交OB於K.
以P為圓心,PK為半徑作圓,交CD於L、M.
分別過M、L作CD的垂線,交圓O於N、R.
10作弧NR的中點S,以SN為半徑將圓O分成17等份.
簡易作法
因為360°/17≈21°10′ ,利用sinA 21°6′=0.3600可得近似角。用該方法作正十七邊形總誤差為17*4′=68′,在不要求十分精確的情況下還是可行的。
作法如下:
1.先畫一條直線,用圓規在上面截取5條相等線段,(儘量越短越好),再截取之前四條線段的和,接續之前畫的線段。這樣,如果每條小線段算作0.1的話,那么整條線段就是1.8。
2.用圓規截取之前5條小線段的長,畫5次,這樣這條線段就是5。1.8/5=0.36。準備工作完畢!
3.另作一條直線,作垂線,1.8的線段作為對邊,5的線段作為斜邊,那個最小的銳角即是近似的360°/17的角。以其頂點為圓心,重複作角直至閉合。畫一大圓,連線其與17條射線的交點,即可。
歷史簡介
最早的十七邊形畫法創造人為高斯。
這其中還有一段趣聞:
1796年的一天,德國哥廷根大學,一個很有數學天賦的19歲青年吃完晚飯,開始做導師單獨布置給他的每天例行的三道數學題。前兩道題在兩個小時內就順利完成了。第三道題寫在另一張小紙條上:要求只用圓規和一把沒有刻度的直尺,畫出一個正17邊形。
他感到非常吃力。時間一分一秒的過去了,第三道題竟毫無進展。這位青年絞盡腦汁,但他發現,自己學過的所有數學知識似乎對解開這道題都沒有任何幫助。困難反而激起了他的鬥志:我一定要把它做出來!他拿起圓規和直尺,他一邊思索一邊在紙上畫著,嘗試著用一些超常規的思路去尋求答案。當視窗露出曙光時,青年長舒了一口氣,他終於完成了這道難題。見到導師時,青年有些內疚和自責。他對導師說:“您給我布置的第三道題,我竟然做了整整一個通宵,我辜負了您對我的栽培……”
導師接過學生的作業一看,當即驚呆了。他用顫抖的聲音對青年說:這是你自己做出來的嗎?青年有些疑惑地看著導師,回答道:是我做的。但是,我花了整整一個通宵。導師請他坐下,取出圓規和直尺,在書桌上鋪開紙,讓他當著自己的面再做出一個正17邊形。青年很快做出了一個正17邊形。導師激動地對他說:你知不知道?你解開了一樁有兩千多年歷史的數學懸案!阿基米德沒有解決,牛頓也沒有解決,你竟然一個晚上就解出來了。你是一個真正的天才!
原來,導師也一直想解開這道難題。那天,他是因為失誤,才將寫有這道題目的紙條交給了學生。每當這位青年回憶起這一幕時,總是說:“如果有人告訴我,這是一道有兩千多年歷史的數學難題,我可能永遠也沒有信心將它解出來”。這位青年就是數學王子高斯。
高斯用代數的方法解決的,他也視此為生平得意之作,還交待要把正十七邊形刻在他的墓碑上,但後來他的墓碑上並沒有刻上十七邊形,而是十七角星,因為負責刻碑的雕刻家認為,正十七邊形和圓太像了,大家一定分辨不出來。
1801年,高斯證明:如果k是費馬數,那么就可以用直尺和圓規將圓周k等分。高斯本人就是根據這個定理作出了正十七邊形,解決了兩千年來懸而未決的難題。
步驟一
給一圓O,作兩垂直的半徑OA、OB,
在OB上作C點使OC=1/4OB,
在OA上作D點使∠OCD=1/4∠OCA作AO延長線上E點使得∠DCE=45度。
步驟二
作AE中點M,並以M為圓心作一圓過A點,
此圓交OB於F點,再以D為圓心,作一圓
過F點,此圓交直線OA於G4和G6兩點。
步驟三
過G4作OA垂直線交圓O於P4,
過G6作OA垂直線交圓O於P6,
則以圓O為基準圓,A為正十七邊形之第一頂點P4為第四頂點,P6為第六頂點。
以1/2弧P4P6為半徑,即可在此圓上截出正十七邊形的所有頂點。
