概周期微分方程
正文
其右端函式對自變數是概周期函式的微分方程;即在方程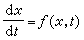 (1)
(1)
對概周期方程(也稱概周期系統)(1),主要是討論其概周期解的存在性和穩定性。線性微分方程是微分方程論的基礎,因此概周期線性微分方程的結構以及概周期解的攝動理論也是概周期系統的重要課題。
線性系統 法瓦爾性質 對概周期線性系統
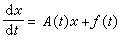 , (2)
, (2)
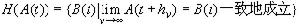 。
。
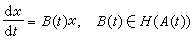 (3)
(3)
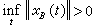 ,
,
弗洛奎特理論 周期線性系統可以通過正則、線性、周期的變換化為常係數線性系統。通常稱這種關係為弗洛奎特理論。人們希望這種性質可以推廣到概周期線性系統或擬周期線性系統。G.R.塞爾指出,弗洛奎特理論不能推廣到概周期線性系統(1974)。
指數型二分性 從第一近似觀點出發,在原點附近的非線性系統
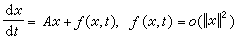 (4)
(4)
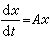 有相同的拓撲結構,原因在於後者具有指數型二分性。對於線性部分為變係數的非線性系統
有相同的拓撲結構,原因在於後者具有指數型二分性。對於線性部分為變係數的非線性系統 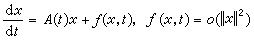 , (5)
, (5)
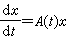 (6)
(6)
非線性系統 對概周期系統 (1)的概周期解的求解,尚無統一的辦法。Z.奧皮爾舉出存在這樣的系統(1),它的解均有界,但沒有概周期解(1961)。A.M.芬克和P.O.弗雷德里克桑構造了一個概周期系統,其每個解都是畢竟有界,但沒有概周期解。由此可見,除了一切解有界以外,還必需附加一些條件,才能得到概周期解。在這方面G.塞費特、塞爾、米爾、J.卡托等人都提出了不同的附加條件。 類似於法瓦爾的考慮,L.阿梅里奧對概周期系統(1)提出分離性的概念,而探討概周期解的存在性。設K是(1)的定義中的緻密集,對任一g(x,t)∈h(ƒ(x,t)),當x(t),y(t)均為
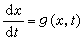 (7)
(7)
討論概周期微分方程要涉及到哈密頓系統以及三體問題。
參考書目
G.E.O.Giacaglia,Perturbation Methods in Nonlinear System,Springer-Verlag,New York,1972.
A.M.Fink,Almost Periodic Differential Equation,Lecture Notes in Math.,377,1974.
A.S.Besicovitch,Almost Periodic Functions,Cambridge Univ.Press,Cambridge,1932.
T.Yoshizawa,Stability Theory and the Existence of Periodic Solution and Almost Periodic Solution,Springer-Verlag,New York,1975.
W.A.Coppel,Dichotomies in Stability Theory,Lec-ture Notes in Math.,6201,1978.