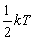基本概念及簡易例子
參見:動能及理想氣體
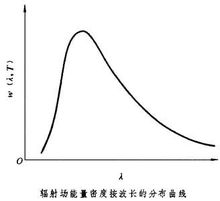
名字裡面的“均分”是指“攤分或類似於攤分”。能量均分定理的原始概念是,當系統平均而言一達到熱平衡時,系統的總動能由各獨立分量所等分。均分定理也為這些能量做出量化的預測。例如它預測惰性氣體的每一個原子,當於溫度T達至熱平衡時,會有平移平均動能(3/2)KBT,其中K為波茲曼常數。隨此引出的是,在等溫時氙的重原子速度會比氦的較輕原子要低。圖二顯示的是四種惰性氣體原子速度的麥克斯韋-波茲曼分布。
在這例子中,關鍵點是動能被速度所二次化。均分定理顯示出於熱平衡時,任何在能量中只以二次出現的自由度(例如是一粒子的位置或速度的一個分量)有著等於½KBT的平均能量,並因此向系統的熱容提供了½K。這個結果有著許多的套用。
平移能量與理想氣體
參見:理想氣體
一粒子質量為m,速度為v,其(牛頓力學)動能為:
其中vx、vy及vz是速度v的直角坐標的分量。這裡,H是哈密頓量,由於哈密頓表述是均分定理一般形式的中心,故下文將以其作為能量的符號。
由於能量是速度各分量的二次方,均分這三分量得每分量在熱平衡時向平均動能提供½kBT。因此粒子的平均動能為(3/2)kBT,跟上面惰性氣體的例子一樣。
更普遍地,理想氣體中的,總能量幾乎全為(平移)動能:假定粒子無內自由度且運動不受其他粒子影響。均分因此預測有N個粒子的理想氣體有平均總能量(3/2) N kBT。
而氣體的熱容則為(3/2) N kB,因此這樣一摩爾氣體的熱容為(3/2)NAkB=(3/2)R,其中NA是阿伏伽德羅常數,而R則是氣體常數。由於R ≈ 2 Cal/(mol·K),均分預測理想氣體的摩爾比熱容約為3 Cal/(mol·K)。這個預測已被實驗證實。
從平均動能可以求出氣體粒子的均方根速度vrms:
其中M = NAm是一摩爾氣體粒子的質量。這個結果對很多套用方面都有用處,例如逸散用的格銳目定律為鈾濃縮提供了一個方法。
鏇轉能量與溶液中的分子滾翻
參見:角速度及鏇轉滲透
在另一個相近的例子中,有一粒子其主轉動慣量I1、I2及I3。它的鏇轉能量是:
其中ω1、ω2及ω3是角速度的主分量。使用跟平移同一套的論證,均分意味著每個粒子的平均鏇轉能量為(3/2)KBT。同樣地,均分使計算出分子平均角速度(更準確來說應是均方根速度)成為可能。
剛性粒子的滾翻——即是分子於溶液中的隨機鏇轉——在核磁共振中觀測到弛緩中有著重要的角色,尤其是在蛋白質核磁共振及剩餘雙極耦合中。 鏇轉滲透可被其他生物物理探測法所觀測到,例如是螢光異向性、流動雙折射及介電質光譜學。
勢能與諧波振盪器
均分定理除可套用於動能外,還能被套用於勢能計算:重要例子包括像彈簧這樣的諧波振盪器,其二次勢能為
其中常數a描述彈簧的韌性,而q則是由平衡導出的。假若這樣一個系統的質量為m,那么它的動能H為½mv=p/2m,其中v及p=mv代表振盪器的速度和動量。聯合這些項可得總能量:
因此均分定理預測在熱平衡時,振盪器有平均能量
其中角括弧代表括弧內的平均量。
這個結果對任何種類的諧波振盪器都是有效的,例如鐘擺,一個振動中的粒子或是被動的電子振盪器。這樣的振盪器在很多情況下都會出現;由均分可得,每個這樣的振盪器都得到一個平均總能量kBT並因此向系統熱容提供kB。這個可以被用於導出熱雜音的公式 及固體摩爾比熱容的杜隆-珀蒂定律公式。後者在均分定理的歷史中尤其重要。
固體的比熱容
均分定理的一個重要套用是在於晶狀固體的比熱容。如此固體的每一個原子都能夠在三個獨立的方向下振盪,因此該固體可以被視為一個擁有各自獨立的3N個簡諧振子的系統,其中N為晶格中的原子數。由於每一個諧振子都有平均能量kBT,所以固體的平均總能量為3NkBT,而比熱容則為3NkB。
如取N為阿伏伽德羅常數NA,並使用R = NAkB這個聯繫氣體常數R及波茲曼常數kB的關係式,可得固體摩爾比熱容的杜隆-珀蒂定律的一個解釋,定律指出晶格中每摩爾的原子熱容為 3R ≈ 6 cal/(mol·K)。
然而,由於量子效應的關係,這條定律在低溫時並不準確;這也不符合實驗導出的熱力學第三定律,第三定律指出摩爾比熱容於絕對零度時必為零。艾爾伯特·愛因斯坦(1907年)及彼得·德拜(1911年)在基礎上加入了量子效應,發展出一套更準確的理論。
許多其他的物理系統可以用一組組的耦合振盪子作為模型。如此振盪子的模型可以被分解成正常模態,這跟鋼琴弦的振動模態及管風琴的共振模態是相近的。另一方面,均分定理被套用於這種系統時一般都會失敗,因為正常模態間是沒有能量交換的。在一個非常的情況下,模態獨立且它們的能量獨立地守恆。這個顯示出有某種的能量混合,正式叫做遍歷性,對於均分定理的成立是十分重要的。
粒子的澱積
參見:澱積、梅森-韋弗爾方程及釀酒
勢能並不一定跟位置成二次關係的。不過,均分定理指出若自由度x只向能量提供x(對一固定實數s而言)的這樣一個倍數,則該部份於熱平衡時的平均能量為kBT/s。
在重力下澱積的這個延伸有一個簡單的套用。例如在啤酒里有時見到的薄霧能由一團團會散射光的蛋白質所組成。 一段時間以後,這些蛋白質團因受重力影響而向下沉澱,使得近底下的部份比頂端的薄霧更多。不過,一個向相合方向作用的過程中,粒子也會向上滲透回到酒瓶的頂部。一達到平衡狀態時,就可以使用均分定理來斷定某一浮力質量mb的蛋白質團的平均位置。對一支瓶高無限的啤酒而言,重力勢能可由下式求出
其中z為蛋白質團的高度,而g則為重力加速度。由於s=1的關係,蛋白質團的平均勢能等於kBT。因此,一個浮力質量為10MDa(大體上為病毒的大小)的蛋白質團會於平衡狀態做出一股2cm高的薄霧。這樣一種往平衡的澱積由梅森-韋弗爾方程所描述。
定量預測
 由能量均分定理得到能量密度曲線
由能量均分定理得到能量密度曲線能量均分定理能夠作出定量預測
。類似於均功定理,對於一個給定溫度的系統,利用均分定理,
可以計算出系統的總平均動能及勢能,從而得出系統的熱容。均分定理還能分別給出能量各個組分的平均值,如某特定粒子的動能又或是一個彈簧的勢能。例如,它預測出在熱平衡時理想氣體中的每個粒子平均動能皆為(3/2)kBT,其中kB為玻爾茲曼常數而T為溫度。更普遍地,無論多複雜也好,它都能被套用於任何處於熱平衡的經典系統中。能量均分定理可用於推導經典理想氣體定律,以及固體比熱的杜隆-珀蒂定律。它亦能夠套用於預測恆星的性質,因為即使考慮相對論效應的影響,該定理依然成立。
 能量均分定理
能量均分定理儘管均分定理在一定條件下能夠對物理現象提供非常準確的預測,但是當量子效應變得顯著時(如在足夠低的溫度條件下),基於這一定理的預測就變得不準確。具體來說,當熱能kBT比特定自由度下的量子能級間隔要小的時候,該自由度下的平均能量及熱容比均分定理預測的值要小。當熱能比能級間隔小得多時,這樣的一個自由度就說成
是被“凍結”了。比方說,在低溫時很多種類的運動都被凍結,因此固體在低溫時的熱容會下降,而不像均分定理原測的一般保持恆定。對十九世紀的物理學家而言,這種熱容下降現象是表明經典物理學不再正確,而需要新的物理學的第一個徵兆。均分定理在預測電磁波的失敗(被稱為“紫外災難”)導致普朗克提出了光本身被量子化而成為光子,而這一革命性的理論對刺激量子力學及量子場論的發展起到了重要作用。
量子效應引起的失敗
當熱能kBT比能階間的差要小得多的時候,均分法則就會失效。均分此時不再成立,是因為能階組成平滑連續能譜的這個假設跟實際情況不近似,而這假設
在上面均分定理推導中有用到。 歷史上,古典均分定理在解釋比熱及黑體輻射時的失敗,對表明需要一套物質及輻射的新理論(即量子力學及量子場論)起了關鍵性的作用。
要說明均分的失效,可考慮一單(量子)諧波振盪子的平均能量,古典個案在上文已討論過。它的量子能階為En=nhν,其中h為普朗克常數,ν為振盪子的基本頻率,而n則為一整數。某指定能階正被置於正則系綜的機率可由其波茲曼因子得出於高溫時,當熱能kBT被能階差hν大得多的時候,指數變數βhν比一要小得多,所以平均能量成了kBT,跟均分定理一致(見圖十)。然而於低溫時,當hν>>kBT的時候,平均能量走向零——高頻能階被“凍結”了(見圖十)。作為另一例子,氫原子內部的受激電子態在室溫下並不提供任何比熱,這是由於熱能kBT(大概是0.025 eV)比最低及下一高能階之間的差(大概是10 eV)要小得多的緣故。
相近的考量可用於任何能階差比熱能大得多的狀況下。例如,
艾爾伯特·愛因斯坦就是用這套論證解決黑體輻射的紫外災難。 由於在一封閉容器下的電磁場有無限個獨立模態,每一個都能被當作諧波振盪器看待,因而就形成了悖論。如果每一個電磁模態皆有平均能量kBT,容器內的能量將為無限大。 然而,根據以上的論證,高ω模態的平均值當ω趨向無限時趨向零;而且描術模態實驗中能量分布的普朗克黑體輻射定律,也是根據同一組論證所中得出的。。
此外,
更微妙的量子效應可引起均分定理的修正,例如全同粒子及連續對稱。全同粒子效應可在非常高密度且低溫時有著顯著的效果。比方說金屬的價電子可以有幾個電子伏的平均能量,正常情況一般對應數萬開爾文的溫度。如此的狀態,密度高得讓泡利不相容原理使得古典門徑無效化,被稱為簡併態費米子氣體。這種氣體對白矮星及中子星的結構很重要。在低溫時,玻色-愛因斯坦凝聚(此凝聚中大量全同粒子占據了低能量態)的費米子類比能夠形成;這種超流體電子是引起超導現象的成因。